How to implement the Neumann boundary condition when solving the heat equation using Chebyshev's pseudo-spectral method

Question

I am studying the Chebyshev pseudo-spectral method and having problems understanding how to implement the Neumann boundary condition when trying to solve a PDE.

To understand better how to implement boundary conditions, I started with the following ODE problem:

$$ y''(x)+ k^2 y(x) = x \tag 1$$ $$ y'(1) = 5 \tag 2$$ $$ y(-1) = 2 \tag 3$$

The solution to this problem is:

$$ y(x) = {\sec(2k)\over k^3 }\Bigg( (2k^3+k) \cos(k - kx) + (5k^2-1) \sin(k + kx) + kx \cos(2k)\Bigg) \tag 4 $$

If we wanted to approximate the solution to this ODE using the pseudo-spectral method, we would first define our problem as:

$$L y_n(x) = f \tag 5$$

where $y_n$ is the approximate numerical solution (vector with $N+1$ elements), the linear operator $L$ is a matrix to be determined (format $N+1 \times N+1$), and $f$ is a vector to be determined. In this case, $f$ is defined as:

$$ f = \begin{bmatrix} 5 & x_2 & x_3 & \cdots & x_N & 2 \end{bmatrix}^T \tag 6$$

while the linear operator $L$ is defined as:

$$ L = \begin{bmatrix} d_{1,1} & d_{1,2} & d_{1,3} &\cdots& d_{1,N} & d_{1,N+1}\\ D_{2,1} & D_{2,2} & D_{2,3} &\cdots& D_{2,N} & D_{2,N+1}\\ D_{3,1} & D_{3,2} & D_{3,3} &\cdots& D_{3,N} & D_{3,N+1}\\ \vdots \\ D_{N,1} & D_{N,2} & D_{N,3} &\cdots& D_{N,N} & D_{N,N+1}\\ 0 & 0 & 0 & \cdots & 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & k^2 & 0 & \cdots & 0 & 0 \\ 0 & 0 & k^2 & \cdots & 0 & 0 \\ \vdots \\ 0 & 0 & 0 & \cdots & k^2 & 0 \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \tag 7$$

where $d_{i,j}$ is the element of Chebychev's differentiation matrix, and $D_{i,j}$ is the element of the squared Chebychev's differentiation matrix. The numerical solution can be computed as:

$$y_n = L^{-1}f \tag 8$$

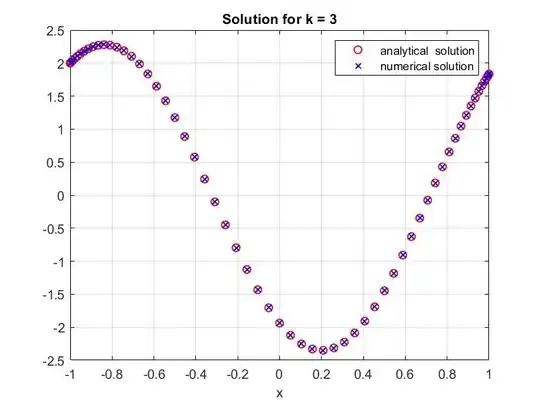
The way I understand the implementation of the boundary conditions, the first and last row of the linear operator $L$ contains the operators on the LHS of the boundary conditions $(2)$ and $(3)$, while the vector $f$ contains the RHS values of those boundary conditions at its first and last row. I confirmed this graphically:

However, I don't understand how to implement the Neumann boundary condition when trying to solve PDE's such as the following heat equation problem:

$$ u_t = u_{xx} \tag 9$$

$$ u(x, 0) = 0 \tag {10}$$

$$ u(1, t) = \sin(t) \tag {11}$$

$$ u_x(-1, t) = 0 \tag {12}$$

Let's say I use the forward fine difference method to solve for time. I need to construct the linear operator $L$ and vector $U_i$ such that:

$$ U_{i+1}=U_{i} + \Delta t \cdot L U_i \tag {13}$$

where $U$ is the numerical solution to the heat equation (format $N+1 \times i_{max}$). The way I thought I should approach this is to simply let $L$ be equal to the squared Chebyshev's differentiation matrix and fix the last row of the vector $U_i$ to $\sin (t_i)$ at each time iteration, just before executing instruction $(13)$. However, I don't know how to implement the Neumann boundary condition. It seems it should be implemented differently than the way I implemented it for the ODE example.

In summary, I don't understand how to implement the Neumann boundary condition numerically when solving the heat equation, so I would like to kindly ask someone to explain it to me. How should I modify $L$ and $U_i$, and why? How does implementing a zero Neumann boundary condition differ from implementing a non-zero one?

Answer 1

Follows a MATHEMATICA script adapted from here which explains all steps needed to apply the method

HeatSpectralMethodSolver[Nx_, Nt_] := Module[{\[Phi], x, t, a, m, n, eqnset, xvalues, tvalues, res, BC1, BC2, BC3, totalEqns, sol, mysol, b1, A, var, avar},
  \[Phi][x_, t_] := Sum[Sum[a[m, n] ChebyshevT[m, x] ChebyshevT[n, t], {n, 0, Nt} ], {m, 0, Nx}];
  (* Defined the Gauss-Lobatto collocation points *)
  xvalues = Table[x[i] -> - Cos[\[Pi] i/Nx], {i, 0, Nx}];
  tvalues = Table[t[i] -> - Cos[\[Pi] i/Nt], {i, 0, Nt}];
  (* Calculate the equation template and BC equations *)
  (* Note the PDE is evaluated at the internal nodes giving (Nx-1)(Ny-1) equations *)
  eqnset = Table[(D[\[Phi][x[i], t[j]], {x[i], 2}] - D[\[Phi][x[i], t[j]], {t[j], 1}] == 0), {i, 1, Nx - 1}, {j, 1, Nt}];
  res = eqnset /. xvalues /. tvalues;
  (* The BCs generate the additional 3(Nx+Ny) equations *)
  BC1 = Table[\[Phi][x[0], t[j]] == 0, {j, 0, Nt}] /. xvalues /. tvalues;
  BC2 = Table[\[Phi][x[Nx], t[j]] == Sin[Pi t[j]], {j, 0, Nt}] /. xvalues /. tvalues;
  BC3 = Table[\[Phi][x[i], t[0]] == 0, {i, 1, Nx - 1}] /. xvalues /. tvalues;
  (* Generate the system of (Nx+1)(Ny+1)equations *)
  totalEqns = Flatten[Join[res, BC1, BC2, BC3]];
  (* Determine the variables in the system of equations *)
  var = Union[Cases[totalEqns, a[_ , _], \[Infinity]]];
  (* Prepare the cofficient matrices for LinearSolve *)
  {b1, A} = CoefficientArrays[totalEqns, var];
  sol = Flatten[LinearSolve[N[A], -N[b1]]];
  (* Evaluate the coefficients a[i,j] *)
  Table[a[i, j] = Partition[sol, Nt + 1][[i + 1, j + 1]], {i, 0, Nx}, {j, 0, Nt}];
  (* Plot the solution *)
  Plot3D[\[Phi][x, t], {x, - 1, 1}, {t, - 1, 1}, AxesLabel -> {"t", "x", "u"}, ColorFunction -> Hue, BoundaryStyle -> Thick, Mesh -> True, ImageSize -> 400, PlotRange -> All]
  ]
HeatSpectralMethodSolver[9, 9]