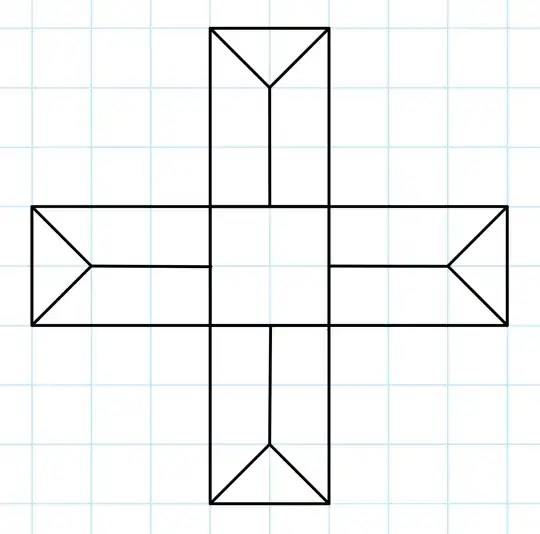
Here is a plane embedding whose dual, even ignoring the unbounded region, cannot be drawn so that all dual vertices are in their corresponding regions, and all dual edges are straight lines:
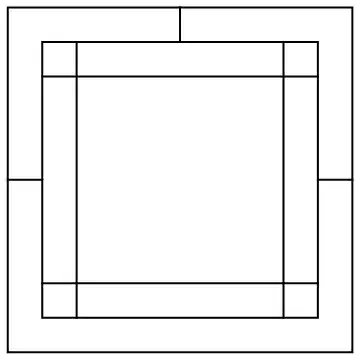
Here is the idea of what goes wrong. This plane embedding has a center square (one region) surrounded by an inner border (8 regions) surrounded by an outer border (3 regions). No matter how we draw the dual vertices and edges for the inner border, they will form an octagon that contains the center square. So the center square (highlighted in red below) is off-limits for the edges connecting the 3 regions of the outer border:
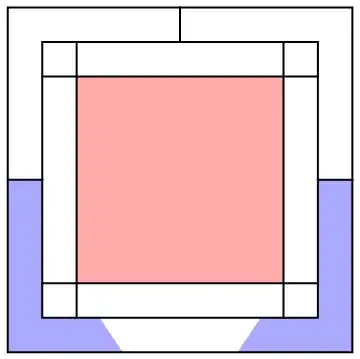
The blue L shape highlighted on the left now represents the portion of the bottom region of the outer border that can "see" the top left region of the outer border without the center square getting in the way. If we pick a dual vertex for the bottom region of the outer border, this is where it must lie, in order for there to be a straight edge to the dual vertex for the top left region.
Similarly, the blue backwards L shape is where the dual vertex for the bottom region must lie in order for there to be a straight edge to the dual vertex for the top right region.
These two blue shapes are disjoint. So it's impossible to pick a location for the dual vertices so that all the dual edges can be drawn as non-intersecting straight lines.