2

Please forgive me if this has already been posted, although I could not find any specific question related enough to my problem (or it might be and I just lack the mathematical background to understand it is).

Assume I have a unit sphere such that $\sum_{i = 1}^n x_i = 1$ and a point $\mathbf{p} = \left[p_1, ..., p_n\right],\, |\mathbf{p}|_2 > 1$ (such that the point lies outside the sphere). If we assume $n=3$ for simplicity, the tangents of the point $\mathbf{p}$ and the unit sphere will form a cone, with a circle on the sphere being the bottom of this cone.

How can I find the hyperplane, as well as its orthogonal vector from the origin describing the "bottom surface" of the cone formed by the tangents of the point and the sphere? Is there a method that holds for arbitrary dimensions?

I believe the question closest to mine is this one (Intersection of hypersphere and hyperplane question), but it does not give me how to find the tangent plane and rather assumes it has already been found.

Thank you!

EDIT As a clarification (see comments) I am referring to the "bottom surface" of the cone that is formed as the tangents of the point and the sphere meet.

To explain more intuitively with a 2-D example: a point outside the unit circle gives two straight lines when drawing them from the point to the surface of the circle and two points on the circle. These two points together form a line, which is our "bottom surface", i.e., a hyperplane in two dimensions, and these three lines then form a triangle in 2 dimensions which would be our "cone" in 3 dimensions.

To explain further, I added a visualization example below in two dimensions, and the vector I am looking for in arbitrary dimensions is "vector describing hyperplane". Hope it helps.

example

Further edit

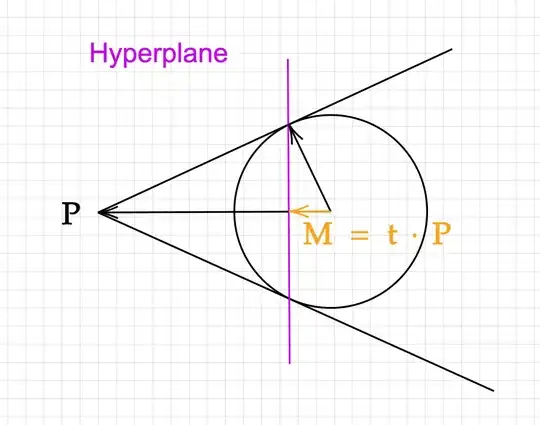
I realize this problem can be described as finding a point $\mathbf{M} = \mathbf{t}\cdot \mathbf{P}$, as the tangent of the vector would be perpendicular to every point it intersects (see image below). However, I am still not sure how to find $\mathbf{t} \in \mathbb{R}$. Intuitively, I know that $|\mathbf{M}| < 1$, since the vector will be inside the hypersphere. Therefore, $\mathbf{t}^2\cdot |\mathbf{P}| < 1$.

Example2

The problem I believe can be seen as an extension to higher dimensions of this question - first finding the points/hyperplane describing the tangent, followed by finding the hyperplane's orthogonal line expressed through $\mathbf{P}$.

Filip
  • 21
  • What do you mean by the "bottom surface"? And which "tangent plane" are you talking about? – Mikhail Katz Nov 06 '23 at 12:17
  • 1
    Let $P$ be the point, $O$ be the center of the (hyper)sphere, and $r$ be the radius of said hypersphere. In our case we have $r = 1$. Find a specific point $M$ on $OP$ such that $OM*OP = r^2$. The proper hyperplane is the one that passes trough $M$ and is orthogonal to $OP$. – user3257842 Nov 06 '23 at 12:20
  • @MikhailKatz Sorry if being unclear; I am referring to the "bottom surface" of the cone that is formed as the tangents of the point and the sphere meet.

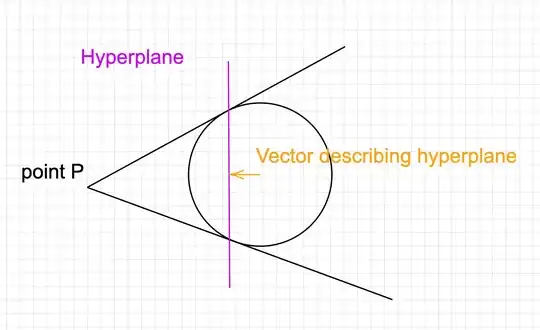
    For a 2-D example: a point outside the unit circle gives two straight lines when drawing them from the point to the surface of the circle and two points on the circle. These two points together form a line, which is our "bottom surface", i.e., a hyperplane in two dimensions, and these three lines then form a triangle in 2 dimensions which would be our "cone" in 3 dimensions.

     – Filip Nov 06 '23 at 12:46
  • SO that's the "Circle on the sphere" that you mentioned in your question? You should edit the question to clarify this. – Mikhail Katz Nov 06 '23 at 12:50
  • @user3257842 if I understand you correctly, that would be one point, which is not exactly what I am looking for, although close. I think $M$ in your case would describe the direction correctly of the hyperplane, but would not be the correct norm, as $M$ should reside inside the sphere unless $\mathbf{p}$ resides exactly on the surface. In other words, we create a hyperplane that divides the sphere in two parts; one towards the point and one beyond it. – Filip Nov 06 '23 at 12:52
  • Okay, thank you @MikhailKatz, I will! :) – Filip Nov 06 '23 at 12:52
  • 1
    Omg yes, I think you are right! What a simple and elegant solution @user3257842! I just have to extra-check this solution, but I think I understand! – Filip Nov 06 '23 at 15:53
  • Let's say the $OP$ segment intersects the sphere at $R$. So we have $|OR| = r$ , and $R$ lies between $O$ and $P$. Now set $M$ such that $|OM| * |OP| = r^2$ . Then $M$ lies between $O$ and $R$ . So the points in order would be $O$ (center of the sphere), $M$ (inside the sphere), $R$ (on the surface of the sphere), $P$ (outside of the sphere). with the lengths obeying $|OM| * |OP| = |OR|*|OR|$ . It is precisely because $|OP| > |OR|$ that we have $|OM| < |OR|$ – user3257842 Nov 06 '23 at 16:02
  • See: https://imgur.com/a/9b1IEoy – user3257842 Nov 06 '23 at 16:03
  • Thank you @user3257842! – Filip Nov 06 '23 at 20:33

0 Answers0