2

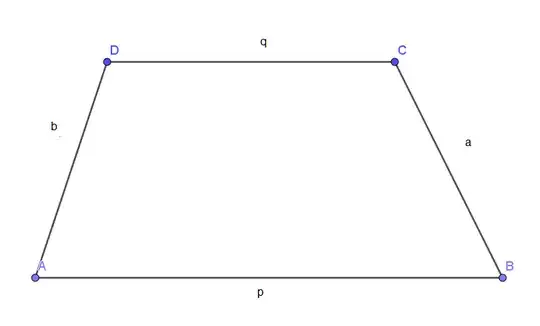
I've been playing with this problem for a long time, but I don't see a solution yet. Consider the sides of a trapezoid of lengths a and b, a > b (not heights) ( see edition (and the bases major "a" and minor "b"). Determine the height of this trapezoid using two different methods. Don't use trigonometry

trapezoid

Can you help me

EDIT Typing error: a and b sides, a and b are not heights, a>b, the bases greatest "p" and least "q" There is also the image that refers to the data

zeros
  • 291
Pamela
  • 121
  • So each base has a corresponding lateral side with equal length? So the quadrilateral is both a trapezoid and a kite? So the quadrilateral is a parallelogram? So $a=b$ which is a contradiction of $a>b$? – peterwhy Oct 17 '23 at 01:51
  • 1
    Not sure I understand the question. Are we saying the four sides have lengths $a,a,b,b$, with the 2nd and 4th sides parallel? And why does the body of the question ask for the height, when the title of the question asks for the area? – Gerry Myerson Oct 17 '23 at 02:36
  • Do you mean you want to compute the area of a generic trapezoid, by knowing only its four sides? If so, see here: https://math.stackexchange.com/q/2637690/255730 – Intelligenti pauca Oct 17 '23 at 13:52
  • It's really helpful to readers to draw and upload a picture of the problem along with the text. – Nate Oct 18 '23 at 05:31
  • Any thoughts about the answer I posted, Pamela? – Gerry Myerson Oct 20 '23 at 11:01

2 Answers2

1

The answer is attached to the edition.

Firstly, it is well-known that we can calculate the height of a triangle with length of its sides fixed. To be specific, consider the fomula $$S=\sqrt{p(p-a)(p-b)(p-c)},p=\frac{a+b+c}{2}.$$ Hence $h_a=2S/a. $

Then for the trapezoid, you can extend the two lateral sides to the intersection and you'll get a small triangle with its sides easily calculated, thus you'll get the height of it. And the height of tragezoid is just some proportion of it.

rushusuixing
  • 595
1

Label the vertices of the trapezoid $C,D,E,F$ so that $|CD|=b$, $|DE|=q$, $|EF|=a$, $|CF|=p$. Drop a perpendicular from $D$ to a point $G$ on $CF$, and one from $E$ to a point $H$ on $CF$. Let $DG=EH=x$, $CG=r,$ $FH=s$ (so $x$ is the height we're trying to find). We have $$ r^2+x^2=b^2,\qquad s^2+x^2=a^2,\qquad r+q+s=p $$ So $s=p-q-r$, so $(p-q-r)^2+x^2=a^2$. Multiply this out, replace $r^2+x^2$ with $b^2$, and solve for $r$, getting $$ r={1\over2}{(p-q)^2-(a^2-b^2)\over p-q} $$ Between this and $x=\sqrt{b^2-r^2}$, you get a formula for $x$ in terms of the givens, $a,b,p,q$.

Gerry Myerson
  • 185,413