11

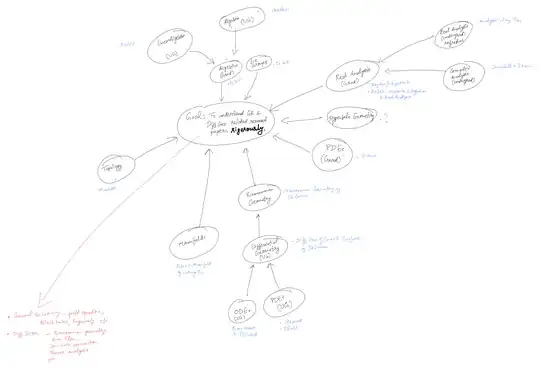
I would like to learn Mathematics for understanding GR, Differential Geometry, Riemannian Geometry and related research papers rigorously.

I would like to carve out a clear path to understand these topics by listing out all the necessary prerequisites.

I have undergrad Math under my belt such as: Real Analysis, Algebra, Topology and ODEs. I am missing intro to PDEs at this point.

I have also created a diagram of the prerequisites in which each bubble represents a subject along with textbooks written in blue.

Please take a look at the attached image/file. UG means "Undergrad" in the diagram.

enter image description here

Specifically, I need help with the following questions:

  1. Is my goal (the center bubble) well defined? I know it may not be specific enough yet, but I have tried to list down some topics I am interested in RED color.
  2. Have I listed all the subjects? Am I missing any subject?
  3. Is Lie Groups worthy of mention here? Or, would it just fit under Algebra?
  4. Is Hyperbolic Geometry worthy of mention here? Is it relevant? How do I learn it? Any textbooks for it?
  5. Would anyone please help me break down the following subjects into specific topics that are necessary for my goal: Manifolds, Riemannian Geometry, Real Analysis (grad version), PDEs (grad version), Algebra (grad version).
Sun
  • 1,124
  • Sean Carroll seems to provide the necessary mathematical elements in his book on general relativity. Also , his lecture notes freely available online. – Vince Vickler Oct 09 '23 at 22:43
  • 1
    I tried reading that. I felt like I was missing some material in between. I could understand it, but I wanted it to be thorough and rigorous mathematically. – Sun Oct 09 '23 at 23:10
  • Yvonne Choquet-Bruhat has a few books that you can look through to guide you. Eventually you'll want to slowly read through Gilbarg-Trudinger for PDEs. Depending on what area of GR you're looking at, there's overlap with the theory of minimal surfaces (e.g. Schoen-Yau's proof of the positive mass theorem). So add in Colding-Minicozzi. – Mr. Brown Oct 10 '23 at 00:52
  • 3
    "I would like to learn Mathematics for understanding GR..." Just to be clear, understanding GR is understanding the physics, not the mathematics alone. You can understand GR without rigorous mathematics and most physicists do not learn it with real mathematical rigor. You could learn all the abstract mathematics without ever really understanding the physical principles, implications and effects this has, which would not really give you an understanding of GR. There's an old saying : "physics is not mathematics". – StephenG - Help Ukraine Oct 10 '23 at 11:14
  • I think hyperbolic geometry and graduate algebra would make good, interesting complements to the material but are certainly not formal prerequisites at all if you only wish to understand DG/GR. – Theo Diamantakis Oct 11 '23 at 13:17

1 Answers1

9

I suggest reading

O’Neill, Barrett, Semi-Riemannian geometry. With applications to relativity, Pure and Applied Mathematics, 103. New York-London etc.: Academic Press. xiii, 468 p. (1983). ZBL0531.53051.

It is 100% rigorous and covers most of what you want to learn, including basics of Lie groups, smooth manifolds and Riemannian geometry. Afterwards, you will likely need to learn hyperbolic geometry, Lie groups and their representations in greater detail, as well as general principal bundles and vector bundles, and connections/curvature on general bundles.

Two more references:

Hall, Brian, Lie groups, Lie algebras, and representations. An elementary introduction, Graduate Texts in Mathematics 222. Cham: Springer (ISBN 978-3-319-13466-6/hbk; 978-3-319-13467-3/ebook). xiii, 449 p. (2015). ZBL1316.22001.

Chapter 1 ("Geometry") of

Jost, Jürgen, Geometry and physics, Berlin: Springer (ISBN 978-3-642-00540-4/hbk; 978-3-642-00541-1/ebook). xiv, 217 p. (2009). ZBL1176.53001.

However, you need a real advisor to guide you.

Moishe Kohan
  • 111,854
  • thank you! What books do you recommend for learning the additional topics that you mentioned? – Sun Oct 09 '23 at 23:10
  • 1
    @Sun: I can, but I think it is premature. It will take you a year to get through O’Neill's book. Chances are, you will not succeed. But I will add few references a bit later. – Moishe Kohan Oct 09 '23 at 23:14
  • Ok a year's worth of material is more than good enough for now. Thank you! – Sun Oct 09 '23 at 23:16