2 lines 1 plane question in 3 dimension

Question

The question I need help with is line $D: x = {y-2\over -1} = z$
line $D': {x-2\over2} = {y-3\over1} = {z+5\over-1}$
Find plane $(α)$ for $(α)$ containing $D$ and the angle between $(α)$ and $D' $ is 60 degrees.

This is what I did let $v,v'$ be the vector for line $D,D'$ respectively. I got $v = ( 1, -1, 1)$ ; $v' = ( 2, 1, -1)$, which is perpendicular (got from their dot product) meaning $D$ and $D'$ is perpendicular.

I calculated that $D$ and $D'$ do not intersect.

Answer 1

A unit normal vector $n=(a,b,c)$ to that plane $(\alpha)$ must be orthogonal to $v$ and make an angle $30^\circ$ with $v'.$ The solutions of $$a^2+b^2+c^2=1,\quad a-b+c=0,\quad|2a+b-c|=\|v'\|\cos(30^\circ)$$ are $$n_1=\pm\frac1{\sqrt2}(1,1,0)\quad\text{and}\quad n_2=\pm\frac1{\sqrt2}(1,0,-1).$$ Using that $(0,2,0)\in D\subset(\alpha),$ we find two planes satisfying the constraints:

$$(\alpha_1):\quad x+y-2=0$$ and $$(\alpha_2):\quad x-z=0.$$

Answer 2

The solutions given by Anne Bauval and Hosam H are very good.

I would like here to take a different approach (a little longer !) based on a general form of the planes passing through line $D$ (equation (2) below).

1. One can write the equations of $D'$ $${x-2\over2} = {y-3\over1} = {z+5\over-1}=\color{red}{t}$$ under the parametric form :

$$D' : \begin{cases}x&=&2\color{red}{t}+2\\y&=&\color{red}{t}+3\\z&=&-\color{red}{t}-5\end{cases}\tag{1}$$

2. Let us now find two points on line $D$, for example $\pmatrix{0\\2\\0}$ and $\pmatrix{2\\0\\2}$. Then, the general equation of planes passing through line $D$ and intersecting $D'$ is, under its determinantal form (see here) :

$$\left|\begin{matrix}0&2&\ \ 2t+2&x\\2&0&\ \ t+3&y\\0&2&-t-5&z\\1&1&1&1\end{matrix}\right|=0$$

Expanding, we obtain :

$$-4x+(-3t-7)y+(-3-3t)z+(6t+14)=0\tag{2}$$

with the alternative form ("pencil of planes") :

$$(-4x-7y-3z+14)+t(-3y-3z+6)=0\tag{2'}$$

From (3), we get a normal vector $N=\pmatrix{-4\\(-3t-7)\\(-3-3t)}$ which has to make a $90°-60°=30°$ angle with $N'=\pmatrix{2\\1\\-1}$, directing vector of line D'.

3. The $30°$ constraint can be transformed into an equation, by using the two ways one can express a dot product :

$$(N.N')^2=\|N\|^2\|N'\|^2 (\cos 30°)^2$$

$$144=(16+(-3t-7)^2+(3+3t)^2) \times 6 \times \frac34$$

giving a quadratic equation whose solutions are

$$t=-1 \ \ \text{and} \ \ t=-7/3.$$

"Plugging" into (1) these values of $t$ gives the equation of the two $(\alpha)$ planes :

$$x-z=0 \ \ \ \text{and} \ \ \ x+y-2=0\tag{3}$$

A remarkable fact is that these planes make a $60°$ between themselves (underlined in the solution by Hosam H). A comparison can be made with the following situation : a book is placed vertically on a table, opened with a 60° angle between its front and back cover (its binding features line $D$); now consider a line on the table (featuring line $D'$) completing an equilateral triangle with the bottom of the book. The line and the two planes are exactly in the same configuration as in the problem.

Fig. 1 : Line $D$ with points $(0,2,0)$ and $(2,0,2)$ (dark green) ; line $D'$ with points corresponding to parameters $t=-1,-7/3$ (yellow) : see equations (1) ; planes (blue and red) given by equations (2) and intermediate plane (grey) corresponding to intermediate value $t=-5/3$, these three planes belonging to the pencil of planes (2') "rotating" around line $D$.

Answer 3

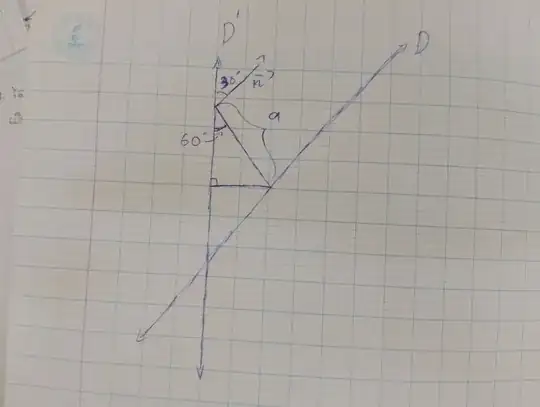
A plane $\pi$ containing line $D$ has its normal vector perpendicular to $D$.

The unit direction vector of $D$ is $\omega =\dfrac{1}{\sqrt{3}}(1, -1, 1) $. Two unit vectors that are perpendicular to $\omega$ are

$ u_1 = \dfrac{1}{\sqrt{2}} (1, 1, 0) $

and

$ u_2 = \omega \times u_1 = \dfrac{1}{\sqrt{6}} (-1, 1, 2) $

So now the unit normal vector $n$ of any plane containing line $D$, can be parameterized by $\theta \in \mathbb{R} $ as follows

$ n = \cos \theta u_1 + \sin \theta u_2 $

Since it is required that line $D'$ makes an angle of $60^\circ$ with the plane, then this means that $D'$ makes an angle of $30^\circ$ with $n$.

The unit direction vector along $D'$ is $\mu = \dfrac{1}{\sqrt{6}}( 2, 1, -1) $

Therefore, it is required that

$ \cos 30^\circ = \mu \cdot n $

Substituting $\mu$ and $n$ and evaluating the dot product we get

$ \cos \dfrac{\pi}{6} = \dfrac{\sqrt{3}}{2} \cos \theta - \dfrac{1}{2} \sin \theta $

The right hand side is just $\cos( \theta + \dfrac{\pi}{6} )$

So by inspection, the solutions are $\theta = 0 $ and $\theta = - \dfrac{\pi}{3} $

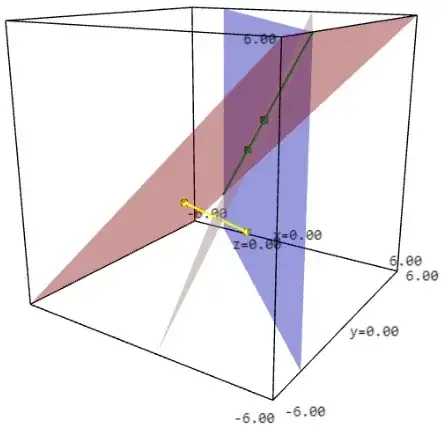
Substituting these two values gives the two possible planes with the desired properties.

The two planes pass through $P_0 = (0,2,0)$ which is on line $D$.

The first normal is

$ n_1 = u_1 = \dfrac{1}{\sqrt{2}}( 1, 1, 0) $

and the second normal is

$n_2 = \dfrac{1}{2 \sqrt{2}} (2, 0, -2) $

Hence the two possible planes are

$ x + y - 2 = 0 $

and

$ x - z = 0 $