5

While testing implementations of Wynn's $\epsilon$-algorithm and Levin's u-transformation I need the value of $$\sum_{n=0}^{\infty} \frac{(-1)^n}{\ln(n+2)} \cdot$$ The results of my algorithms are in agreement with the Pari/GP sumalt value of $0.92429989722293885595957$. But Wolfram Alpha gives the following approximated sum when entering 

sum (-1)^n/(ln(n+2))

(a direct link from Math.SE will be mangled and does not work, here is the eq.):

$$\sum_{n=0}^{\infty}\dfrac{(-1)^n}{\log(2+n)}\approx1.00766524110155\ldots$$

Questions:

  • Are the values from Pari and my algorithms correct?
  • Is there a closed form analytical result?
gammatester
  • 19,147
  • Concerning pari/gp's function sumalt (which will often return finite result even for divergent series) a trick is to gradually increase precision ( \p 100 and more) : the correct digits should remain as precision increases. – Raymond Manzoni Dec 15 '13 at 09:01
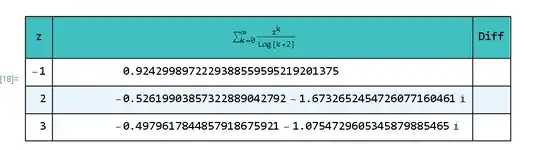
  • @Manu: Thank you for the info. I tested it on Raspberry Pi with a[n_] := 1/Log[n + 2]; EulerTransformation[0, 20] and can reproduce your result. But the result is always displayed with 4 digits even for error $\approx 10^{-8}$ and for nmax_ >= 22 I get obscure errors. – gammatester Jun 26 '17 at 16:22
  • @TeM: This is equivalent to Pari/GP's sumalt. – gammatester Jun 27 '17 at 10:25

3 Answers3

6

For $x \in (0,1)$ consider

$$f(x) = \sum_{n=2}^{\infty} \frac{(-1)^n}{\log{(n+2)}} x^{\log{(n+2)}}$$

Then

$$f'(x) = \frac{1}{x} \left [ 1-\left(1-2^{1+\log{x}}\right) \zeta(-\log{x})\right]$$

where $\zeta$ is the Riemann zeta function. Using $f(0)=0$, I get that the sum may be expressed in terms of the following integral:

$$\int_0^{\infty} du \left [ 1-\left ( 1 - \frac{1}{2^{u-1}}\right ) \zeta(u)\right]$$

Ron Gordon
  • 141,538
  • Nice and tricky! But I guess your lower summation limit is 0? – gammatester Aug 26 '13 at 13:23
  • @gammatester: I added and subtracted the $n=1$ term in the sum to get the zeta function; I hope I answered your question. – Ron Gordon Aug 26 '13 at 13:24
  • Thank you for the final integral. I evaluated it with Pari and got the 0.92429989722293885595957 again. I will accept your answer because of the analytical result (and up-vote Artin's, and I hope I will avoid multipart questions in the future). – gammatester Aug 26 '13 at 14:01
  • @gammatester: thanks. I like the integral representation because the series converges incredibly slowly. – Ron Gordon Aug 26 '13 at 14:37
1

Since $\frac{1}{\log 2}-\frac 1{2\log 3}<1$ already, there is no way $1.07\dots$ can be anywhere close. To get high precision by hand, use Euler-Maclaurin. With Wolfram Alpha, I got $1.01845-2.45012\cdot 10^{-13}i$ . Remember, however, that WA was designed to impress calculus students and educators, not for any minimally non-trivial task...

fedja
  • 19,348
0

some values.. enter image description here

with z=1 agree with your calculation pole in z=1 and the rest analitic continuation

user547221
  • 357