Is there an expression for $I(n)=\int_{0}^{\frac{\pi}{4}}x\tan^{n}x dx$?

Question

I've played around a little with this integral, and I can straightforwardly evaluate it with a substitution $\tan x\mapsto x$ in terms of the Beta function if the bounds were $(0,\pi /2)$. But for the bounds $(0,\pi /4)$ the substitution takes the bounds to $(0,1)$ which can't be done with the Beta function.

Alternatively, if we substitute $\tan 2x \mapsto x$, we get that $$I(n)=\frac{1}{4}\int\limits_{0}^{\infty}\frac{\left(\sqrt{x^{2}+1}-1\right)^{n}\tan^{-1}x}{x^{n}\left(1-x^{2}\right)}dx=\frac{1}{4}\int\limits_{0}^{\infty}\frac{x^{n}\tan^{-1}x}{\left(1-x^{2}\right)\left(\sqrt{x^{2}+1}+1\right)^{n}}dx$$

I'm wondering if there is a nice expression for this integral.

Side note, I'm only actually interested in what it is for $n\geq1$.

---

Checking with Wolfram Alpha, it seems that the integral behaves slightly differently for odd and even $n$.

For $n=2k-1$,

$k$	$n$	$I(2k-1)$
$1$	$1$	$\frac{1}{2}G-\frac{\pi}{8}\ln 2$
$2$	$3$	$-\left(\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{1}{4}\pi+\frac{1}{2}\right)$
$3$	$5$	$\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{1}{4}\pi+\frac{2}{3}$
$4$	$7$	$-\left(\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{1}{3}\pi+\frac{73}{90}\right)$
$5$	$9$	$\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{1}{3}\pi+\frac{284}{315}$
$6$	$11$	$-\left(\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{23}{60}\pi+\frac{3103}{3150}\right)$
$7$	$13$	$\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{23}{60}\pi+\frac{54472}{51975}$
$9$	$15$	$-\left(\frac{1}{2}G-\frac{\pi}{8}\ln 2-\frac{44}{105}\pi+\frac{10459489}{9459450}\right)$

(where $G$ is Catalan's constant.)

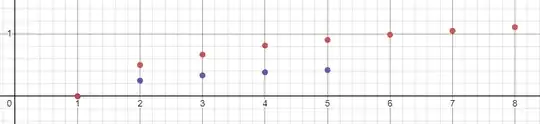
$I(n)$ for odd $n$ takes the form of $(-1)^{k-1}\left(\frac{1}{2}G-\frac{\pi}{8}\ln 2-p_{k}\pi+q_{k}\right)$ where $p$ and $q$ form some kind of sequence of rational numbers.

If we plot a graph of $p_{k}$ (purple) and $q_{k}$ (red) against $k$, we get something that looks like a logarithm but is also not really:

---

Whereas for $n=2k$,

$k$	$n$	$I(2k)$
$1$	$2$	$\frac{1}{4}\pi-\frac{1}{32}\pi^{2}-\frac{1}{2}\ln 2$
$2$	$4$	$-\left(\frac{1}{6}+\frac{1}{6}\pi-\frac{1}{32}\pi^{2}-\frac{2}{3}\ln2\right)$
$3$	$6$	$\frac{13}{60}+\frac{13}{60}\pi-\frac{1}{32}\pi^{2}-\frac{23}{30}\ln 2$
$4$	$8$	$-\left(\frac{29}{105}+\frac{19}{105}\pi-\frac{1}{32}\pi^{2}-\frac{88}{105}\ln2\right)$
$5$	$10$	$\frac{2333}{7560}+\frac{263}{1260}\pi-\frac{1}{32}\pi^{2}-\frac{563}{630}\ln 2$

The first thing I noticed was the denominator. If we make them the same each time, we get

$k$	$n$	$I(2k)$
$1$	$2$	$\frac{1}{4}\pi-\frac{1}{32}\pi^{2}-\frac{2}{4}\ln 2$
$2$	$4$	$-\left(\frac{1}{6}+\frac{1}{6}\pi-\frac{1}{32}\pi^{2}-\frac{4}{6}\ln2\right)$
$3$	$6$	$\frac{13}{60}+\frac{13}{60}\pi-\frac{1}{32}\pi^{2}-\frac{46}{60}\ln 2$
$4$	$8$	$-\left(\frac{29}{105}+\frac{19}{105}\pi-\frac{1}{32}\pi^{2}-\frac{88}{105}\ln2\right)$
$5$	$10$	$\frac{2333}{7560}+\frac{1578}{7560}\pi-\frac{1}{32}\pi^{2}-\frac{6756}{7560}\ln 2$

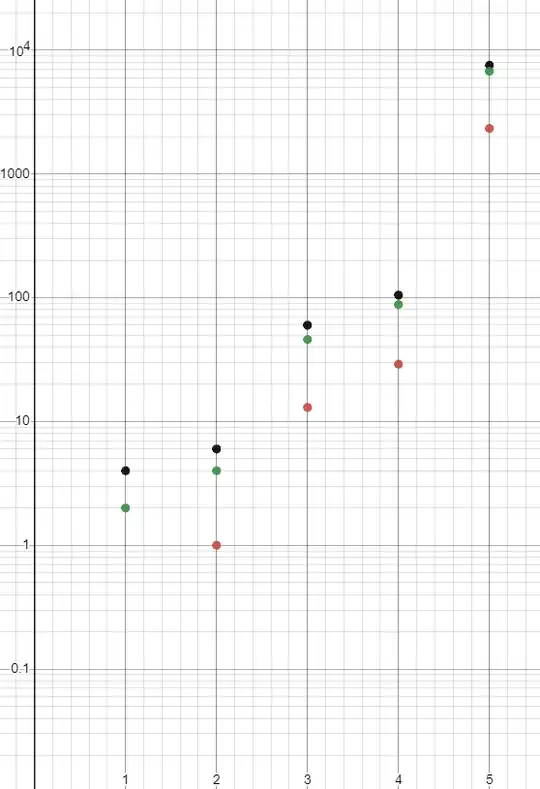
Which indicates that $I(n)$ for even $n$ takes the form of $(-1)^{k-1}\left(-\frac{1}{32}\pi^{2}+\frac{1}{r_{k}}\left(a_{k}+b_{k}\pi-c_{k}\ln{2}\right)\right)$ where $r,a,b,c$ form a sequence in the natural numbers.

Plotting $r$ (black), $b$ (blue) and $c$ (green) against $k$ yields these exponential graphs:

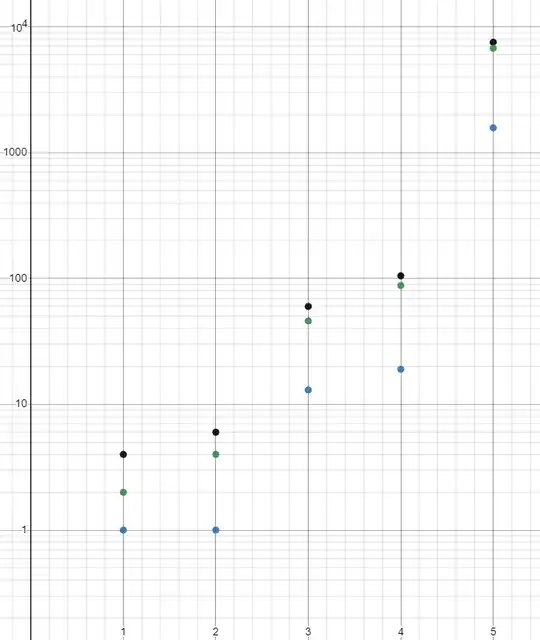
But $a_{1}=0$, and its graph (red) looks like this:

Seems like they're in pairs, but I also fail to see any relation between the numbers at all.

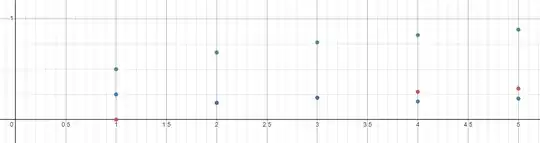
If we plot $\frac{a}{r},\frac{b}{r},\frac{c}{r}$ against $k$, we get

We see that $\frac{b}{r}$ approaches some value around $0.19$.

---

None of the number sequences mentioned above show up on OEIS.

I have been stuck here for a few days, and any insight would be highly welcomed.

Kisaragi Ayami

Answer 1

This is the final formula I got in terms of no special functions and only finite summations, $$\boxed{I(2n)=\left(-1\right)^{n}\left(\left(-1\right)^{1+n}\frac{\pi}{4}\sum_{i=1}^{n}\frac{\left(-1\right)^{i}}{2\left(n-i\right)+1}+\frac{\pi^{2}}{32}+\frac{1}{2}\sum_{i=0}^{n-1}\left(\frac{1}{2\left(n-i-1\right)+1}\sum_{k=1}^{n-1-i}\frac{\left(-1\right)^{k}}{k}\right)+\frac{\ln2}{2}\sum_{i=1}^{n}\frac{1}{2i-1}\right)}$$ Checks out numerically for smaller values.

---

$$I(n)=\int\limits_{0}^{\pi/4}x\tan^{n}x dx$$

Absolute Value of Coefficient of "$\ln\left(2\right)$" in the case of $I(2k)$ is, $$\boxed{\frac{\psi^{(0)}\left(k+\frac{1}{2}\right)}{4}+\frac{\ln2}{2}+\frac{\gamma}{4}}$$ which follows the recurrence relation, $$f(n+1)=f(n)+\frac{1}{4n+2}$$

Absolute Value of Coefficient of "$\pi$" in the case of $I(2k)$ is, $$\boxed{\frac{\pi}{16}-\frac{\left(-1\right)^{k}}{8}\Phi\left(-1,1,k+\frac{1}{2}\right)}$$ or, $$\frac{\pi}{16}-\frac{\left(-1\right)^{k}}{8}\int_{0}^{\infty}\frac{e^{-\left(k+\frac{1}{2}\right)x}}{1+e^{-x}}dx$$ which follows the recurrence relation, $$f(n+1)=f(n)+\frac{(-1)^n}{8n+4}$$

Therefore, $$I(2n)=\left(-1\right)^{n+1}\left(F_n+\frac{\pi^{2}}{32}-\frac{\pi}{8}\left(-1\right)^{n}\int_{0}^{\infty}\frac{e^{-\left(n+\frac{1}{2}\right)x}}{1+e^{-x}}dx-\frac{\psi^{(0)}\left(n+\frac{1}{2}\right)}{4}\ln2-\frac{\ln^{2}2}{2}-\frac{\gamma}{4}\ln2\right)$$ where, $F_n$ is the Rational Term (Taken as Positive).

Cannot find the recurrence relation for $F_n$, but trying.
Also if someone has a closed form for the Lerch's Transcendent for these specific values do tell.
I will also just list down some values of $F_n$. $$0,\frac{1}{6},\frac{13}{60},\frac{29}{105},\frac{2333}{7560},\frac{3578}{10395},\frac{397753}{1081080},\frac{265702}{675675},\frac{75700799}{183783600}$$

EDIT:
I will also mention it in terms of summations without any special functions, $$I(2n)=\left(-1\right)^{n+1}\left(F_n+\frac{\pi^{2}}{32}-\frac{\pi}{4}\left(-1\right)^{n}\sum_{i=0}^{\infty}\frac{\left(-1\right)^{i}}{\left(2n+1+2i\right)}-\frac{\ln2}{2}\sum_{i=1}^{n}\frac{1}{2i-1}\right)$$ EDIT 2:
The recurrence relation for $F_n$ has been found, $$F_{n+1}=F_n-\frac{1}{4n+2}\sum_{k=1}^{n}\frac{\left(-1\right)^{k}}{k}$$

Although closed form for this might be hard to get.
But we can write this as a Double Summation, $$F_{n+1}=-\frac{1}{2}\sum_{i=0}^{n}\left(\frac{1}{2\left(n-i\right)+1}\sum_{k=1}^{n-i}\frac{\left(-1\right)^{k}}{k}\right)$$

Answer 2

Based on the definition of $I_n$, we observe that $$ I_n+I_{n+2} {= \int_0^\frac{\pi}{4}x\tan^nx(1+\tan^2x)dx \\= \frac{x\tan^{n+1}x}{n+1}\Big|_0^\frac{\pi}{4}-\int_0^\frac{\pi}{4}\frac{\tan^{n+1}x}{n+1}dx \\= \frac{\pi}{4n+4}-\int_0^\frac{\pi}{4}\frac{\tan^{n+1}x}{n+1}dx \\= \frac{\pi}{4n+4}-\int_0^1\frac{x^{n+1}}{(n+1)(1+x^2)}dx. } $$ We split the cases of even and odd values of $n$. For $n=2k$ we have $$ \int_0^1\frac{x^{n+1}}{(n+1)(1+x^2)}dx {= \int_0^1\frac{x^{2k+1}}{(2k+1)(1+x^2)}dx \\= \frac{1}{2}\int_0^1\frac{x^k}{(2k+1)(1+x)}dx \\= \frac{1}{2}\int_0^1\frac{x^k-(-1)^k+(-1)^k}{(2k+1)(1+x)}dx \\= \frac{(-1)^k\ln2}{4k+2} + \int_0^1\sum_{i=0}^{k-1}\frac{x^{k-i-1}(-1)^i}{4k+2}dx \\= \frac{(-1)^k\ln2}{4k+2} + \sum_{i=0}^{k-1}\frac{(-1)^i}{(4k+2)(k-i)}. } $$ Similarly for $n=2k-1$ we obtain $$ \int_0^1\frac{x^{n+1}}{(n+1)(1+x^2)}dx {= \int_0^1\frac{x^{2k}-(-1)^k+(-1)^k}{2k(1+x^2)}dx = \frac{(-1)^k\pi}{8k} + \sum_{i=0}^{k-1}\frac{(-1)^i}{2k(2k-2i-1)}. } $$ Therefore, $${ I_{2k}+I_{2k+2}= \frac{\pi}{8k+4}-\frac{(-1)^k\ln2}{4k+2} - \sum_{i=0}^{k-1}\frac{(-1)^i}{(4k+2)(k-i)} \\ I_{2k-1}+I_{2k+1}= \frac{\pi[1-(-1)^k]}{8k} - \sum_{i=0}^{k-1}\frac{(-1)^i}{2k(2k-2i-1)}. } $$ The latter two equations confirm your numerical achievement on saying $I_{2k-1}=(-1)^{k-1}\left(\frac{G}{2}-\frac{\pi\ln 2}{8}-p_k\pi+q_k\right)$. In fact, replacing this expression in $I_{2k-1}+I_{2k+1}$ yields $$ { (-1)^{k-1}\left(\frac{G}{2}-\frac{\pi\ln 2}{8}-p_k\pi+q_k\right) + (-1)^{k}\left(\frac{G}{2}-\frac{\pi\ln 2}{8}-p_{k+1}\pi+q_{k+1}\right) \\= \frac{\pi[1-(-1)^k]}{8k} - \sum_{i=0}^{k-1}\frac{(-1)^i}{2k(2k-2i-1)} \\\implies (p_k-p_{k+1})\pi-q_k+q_{k+1} = \frac{\pi[(-1)^k-1]}{8k} - \sum_{i=0}^{k-1}\frac{(-1)^{k+i}}{2k(2k-2i-1)} \\\implies p_k-p_{k+1} = \frac{(-1)^k-1}{8k} \quad,\quad q_k-q_{k+1} = \sum_{i=0}^{k-1}\frac{(-1)^{k+i}}{2k(2k-2i-1)}, } $$ where $p_1=q_1=0$. As for even values of $n$ ($n=2k$), by replacing $I_{2k}=(-1)^{k-1}\left(-\frac{\pi^2}{32}+a_k+b_k\pi-c_k\ln2\right)$ we achieve $$ { (-1)^{k-1}\left(-\frac{\pi^2}{32}+a_k+b_k\pi-c_k\ln2\right) + (-1)^{k}\left(-\frac{\pi^2}{32}+a_{k+1}+b_{k+1}\pi-c_{k+1}\ln2\right) \\= \frac{\pi}{8k+4}-\frac{(-1)^k\ln2}{4k+2} - \sum_{i=0}^{k-1}\frac{(-1)^i}{(4k+2)(k-i)} \\\implies a_{k+1}+b_{k+1}\pi-c_{k+1}\ln2 - (a_k+b_k\pi-c_k\ln2) \\= \frac{\pi(-1)^k}{8k+4}-\frac{\ln2}{4k+2} - \sum_{i=0}^{k-1}\frac{(-1)^{k+i}}{(4k+2)(k-i)} \\\implies a_{k+1}-a_k = - \sum_{i=0}^{k-1}\frac{(-1)^{k+i}}{(4k+2)(k-i)} \quad,\quad b_{k+1}-b_{k} = \frac{(-1)^k}{8k+4} \quad,\quad c_{k+1}-c_k = \frac{1}{4k+2}, } $$ where $a_1=0$, $b_1=\frac{1}{4}$ and $c_1=\frac{1}{2}$. We arrive at two interesting closed-forms: $$ \boxed{ { \int_0^\frac{\pi}{4}x\tan^{2k}xdx = \frac{\pi^2(-1)^k}{32}+(-1)^k\sum_{l=0}^{k-1}\left(\frac{(-1)^{l-1}\pi}{8l+4}+ \frac{\ln2}{4l+2} + \sum_{i=1}^{l}\frac{(-1)^{i}}{i(4l+2)}\right), \\ \int_0^\frac{\pi}{4}x\tan^{2k-1}xdx = \frac{G(-1)^{k-1}}{2}+\frac{(-1)^{k}\pi\ln 2}{8}+(-1)^k\sum_{l=1}^{k-1}\left(\frac{\pi\sin^2\frac{\pi l}{2}}{4l}+ \sum_{i=1}^{l}\frac{(-1)^{i}}{2l(2i-1)}\right). } } $$

Answer 3

This is a collection of my attempts so far to solve this interesating problem.

Original post

This is not a closed expression for the integral but for the generating function of the integrals.

I asked Mathematica to find the generating function

$$g(z) = \sum_{k=0}^{\infty} I(n) z^n\tag{1}$$

for the integral in question

$$I(n) = \int_{0}^{\frac{\pi}{4}}x (\tan{x})^n\tag{2}$$

doing the summation under the integral which leads to this integral

$$g(z) = \int_{0}^{\frac{\pi}{4}}\frac{x}{1-z \tan{x}}\tag{3}$$

And Mathematica replied with this closed expression

$$\begin{align} g(z) = \frac{1}{32 \left(z^2+1\right)}\left(-16 i z \text{Li}_2\left(e^{-2 i \cot ^{-1}(z)}\right)+16 i z \text{Li}_2\left(i e^{-2 i \cot ^{-1}(z)}\right)\\ -16 z \log \left(z^2+1\right) \cot ^{-1}(z)+i \pi ^2 z+24 i \pi z \cot ^{-1}(z)\\ -32 z \cot ^{-1}(z) \log \left(1-e^{-2 i \cot ^{-1}(z)}\right)+32 z \cot ^{-1}(z) \log \left(1-i e^{-2 i \cot ^{-1}(z)}\right)\\ -8 \pi z \log \left(1-i e^{-2 i \cot ^{-1}(z)}\right)\\ -32 z \cot ^{-1}(z) \log \left(\cos \left(\cot ^{-1}(z)+\frac{\pi }{4}\right)\right)+\pi ^2\right)\end{align}\tag{4}$$

Hence we should have

$$I(n) = \frac{1}{n!}\frac{d^n}{dz^n}g(z)|_{z\to 0}\tag{5}$$

I have checked that $(5)$ holds for $n=1..15$ with $I(n)$, defined by $(2)$, calculated with Mathematica.

EDIT

I was able to simplify the expression $g(z)$ resulting in the equivalent g.f.

$$\begin{align} g_1(z) = &\frac{1}{32 \left(z^2+1\right)}(\pi^2-5 i \pi ^2 z-4 \pi z \log (2)-8 \pi z \log (1-z)\\& +8 \pi z \log (z+i)+16 i z \left(\text{Li}_2\left(i \frac{ z-i}{i+z}\right)-\text{Li}_2\left(\frac{z-i}{i+z}\right)\right)) \end{align}\tag{6}$$

Although it is not obvious $g_1(z)$ is a real function (as it should be per definitionem).

EDIT 2

Here is the expression with is explicitly real since, for real z, it is identical to its complex conjugate

$$\begin{align}g_2(z) = &\frac{1}{32 \left(1+z^2\right)}\left(\pi ^2 - 8 \pi z \log (1-z)+4 \pi z \log \left(\frac{1}{2} \left(1+z^2\right)\right)\\ +8 i z \left(\text{Li}_2\left(\frac{i (z-i)}{i+z}\right)-\text{Li}_2\left(\frac{z-i}{i+z}\right)\\ -\text{Li}_2\left(-\frac{i (z+i)}{-i+z}\right)+\text{Li}_2\left(\frac{z+i}{-i+z}\right)\right)\right)\end{align}\tag{7}$$

EDIT 3

I found another interesting representation of the integral as an infinite sum

$$I(n) = -\frac{1}{16} \pi \left(H_{\frac{n-3}{4}}-H_{\frac{n-1}{4}}\right)+\frac{1}{4} \sum _{k=0}^{\infty } \frac{(-1)^{k+1} \left(H_{\frac{1}{4} (2 k+n)}-H_{\frac{1}{4} (2 k+n-2)}\right)}{2 k+n+1}\tag{8}$$

Here $H_z$ is the harmonic number.

EDIT 4

Here is my result for the integral in terms of finite sums. The idea was followed here before.

I started from integration by parts to get rid of the factor $x$ in the integrand:

$$i_i(n) :=\int_{0}^{\frac{\pi}{4}} x \tan(x)^n\;dx=\frac{\pi}{4}f(n) - F(n)\tag{4.1}$$

where

$$f(n,x) = \int_{0}^{x}\tan(y)^n\;dy\tag{4.2a}$$ $$f(n) = f(n,x\to \frac{\pi}{4})\tag{4.2b}$$ $$F(n) = \int_{0}^{\frac{\pi}{4}}f(n,x)\;dx\tag{4.2c}$$

Now, instead of calculating $f$ and $F$ for all $n$, we employ recursion.

The basic recursion

$$f(n,x) = \frac{1}{n-1}\tan(x)^{n-1}-f(n-2,x)\tag{4.3a}$$

holding for $n \ge 2$ follows directly from the properties of $\tan(x)$ as can be shown by integrating the equation

$$\begin{align}\frac{d}{dx}\frac{\tan(x)^{n-1}}{n-1}=\tan(x)^{n-2}\frac{d}{dx}\tan(x)=\tan(x)^{n-2}\frac{1}{\cos(x)^2}\\ =\tan(x)^{n-2}(1+\tan(x)^2)=\tan(x)^{n-2}+\tan(x)^{n}\end{align}$$

between $0$ and $x$.

Letting $x\to \frac{\pi}{4}$ in $(4.3a)$ and observing $(4.2b)$ gives the first recursion

$$f(n) = \frac{1}{n-1}-f(n-2)\tag{4.3b}$$

Integrating $(4.3a)$ between $0$ and $\frac{\pi}{4}$ and observing $(4.2c)$ gives the second recursion

$$F(n)=\frac{f(n-1)}{n-1}-F(n-2)\tag{4.3c}$$

In order to solve the recursions we need the inital values of the quantities, jointly called $q(n)$ here, for $n=0$ and $n=1$ where $q(0)$ is needed to calculate $q(n)$ for even $n \ge 2$, and $q(1)$ to calculate the $q(n)$ for odd $n \ge 3$.

The inital values are the only quantities which require integration, and they are given by

$$f(0) = \int_{0}^{\frac{\pi}{4}} \tan(x)^0 \;dx= \frac{\pi}{4}\tag{4.4a}$$ $$f(1) = \int_{0}^{\frac{\pi}{4}} \tan(x)^1 \;dx=-\log(\cos(x))|_{0}^{\frac{\pi}{4}}=\frac{\log(2)}{2}\tag{4.4b}$$ $$F(0) = \int_{0}^{\frac{\pi}{4}}\;dx \int_{0}^{x} \tan(y)^0 \;dy=\int_{0}^{\frac{\pi}{4}} x \;dx =\frac{\pi^2}{32}\tag{4.4c} $$ $$F(1) = \int_{0}^{\frac{\pi}{4}}\;dx \int_{0}^{x} \tan(y)^1 \;dy=\int_{0}^{\frac{\pi}{4}}(-\log(\cos(x)))\;dx\\ =\frac{\pi}{4}\log(2)-\frac{1}{2} G \;\;\text{(G=Catalan's constant)} \tag{4.4d} $$

We shall derive $(4.4d)$ later.

Now the solutions are easy to find considering e.g.

$$f(2) = \frac{1}{2-1} - f(0) = 1 - \frac{\pi}{4}$$ $$f(4) = \frac{1}{4-1} - f(2) = \frac{1}{3}-1+\frac{\pi}{4}$$ $$f(6) = \frac{1}{6-1} - f(4) = \frac{1}{5}-\frac{1}{3}+1-\frac{\pi}{4}$$ ...

and

$$f(3) = \frac{1}{3-1} - f(1) = \frac{1}{2} - \frac{\log(2)}{2}$$ $$f(5) = \frac{1}{5-1} - f(3) = \frac{1}{4}-\frac{1}{2} + \frac{\log(2)}{2}$$ $$f(7) = \frac{1}{7-1} - f(5) = \frac{1}{6}-\frac{1}{4}+\frac{1}{2} - \frac{\log(2)}{2}$$ ...

and similarly for $F$.

These expansions are easily generalized with this final result for $n$ even and $n$ odd, respectively (calling $i_s(n)$ the representation of the integral $i(n)$ as (finite) sums)

$$\boxed {\begin{align}i_s(n \;\text{even})=(-1)^{n/2} \left(\frac{\pi ^2}{32}+\sum _{j=1}^{\frac{n}{2}} \frac{\sum _{m=1}^{j-1} \frac{(-1)^m}{2 m}}{2 j-1}\\ +\frac{\pi}{4} \sum _{j=1}^{\frac{n}{2}} \frac{(-1)^j}{2 j-1}+\frac{\log (2)}{2} \sum _{j=1}^{\frac{n}{2}} \frac{1}{2 j-1}\right)\end{align} }\tag{4.5a}$$

$$\boxed{ \begin{align} i_s(n \;\text{odd})=(-1)^{\frac{n-1}{2}} \left(\frac{G}{2}-\frac{\pi}{8}\log (2)-\sum _{j=1}^{\frac{n-1}{2}} \frac{\sum _{m=1}^j \frac{(-1)^m}{2 m-1}}{2 j}\\ +\frac{1}{4} \pi \sum _{j=1}^{\frac{n-1}{2}} \frac{(-1)^j-1}{2 j}\right) \end{align} }\tag{4.5b}$$

Derivation of expression for $F(1)$ by $(4.4d)$

We can write

$$\begin{align} -\log (\cos (x))=-\log \left(\frac{1}{2} \left(e^{i x}+e^{-i x}\right)\right)=-\log \left(\frac{1}{2} \left(e^{i x}(1+e^{-2i x}\right)\right)\\ =\log (2)-i x-\log \left(1+e^{-2 i x}\right)=\log (2)-i x-\sum _{k=1}^{\infty } \frac{(-1)^{k-1} e^{-2 i k x}}{k} \end {align}$$

integrating gives

$$ \int_{0}^{\frac{\pi}{4}}(-\log (\cos (x)))\;dx \\= \frac{\pi}{4}\log(2)- i \frac{\pi^2}{32}-\sum _{k=1}^{\infty }\frac{i e^{\frac{i \pi k}{2}} \left(-1+e^{\frac{i \pi k}{2}}\right)}{2 k^2} \\= \frac{\pi}{4}\log(2)- i \frac{\pi^2}{32}-\sum _{k=1}^{\infty }\frac{\sin \left(\frac{\pi k}{2}\right)}{2 k^2}+\sum _{k=1}^{\infty }\frac{\sin (\pi k)}{2 k^2} \\ +i \sum _{k=1}^{\infty }\frac{\cos \left(\frac{\pi k}{2}\right)}{2 k^2}-i\sum _{k=1}^{\infty } \frac{\cos (\pi k)}{2 k^2} \\= \frac{\pi}{4}\log(2)- i \frac{\pi^2}{32} -\frac{1}{2}(1-\frac{1}{3^2}+\frac{1}{5^2}\mp...) +0-i\frac{\pi ^2}{96}+\frac{i \pi ^2}{24} \\ =\frac{\pi}{4}\log(2)-\frac{1}{2}G $$

which completes the derivation.

Answer 4

$\def\F{\text F}$

Split using binomial theorem:

$$\int_0^\frac\pi4x\tan^n(x)dx=\int_0^\frac\pi4x\sin^n(x)\sec^n(x)dx=\sum_{k=0}^n\binom nk\left(\frac i2\right)^n(-1)^k\int_0^\frac\pi4x e^{(2k-n)ix}\sec^n(x)dx$$

Using integration by parts or Wolfram Alpha gives the hypergeometric function:

$$\int xe^{irx}\sec^n(x)dx=\sec^n(x)\frac{(e^{2ix}+1)^ne^{irx}}{(n+r)^2}\left(\,_3\F_2\left(n,\frac{n+r}2,\frac{n+r}2;\frac{n+r}2+1; \frac{n+r}2+1;-e^{2i x}\right)-ix(n+r)\,_2\F_2\left(n,\frac{n+r}2;\frac{n+r}2+1;-e^{2ix}\right)\right)$$

The final hypergeometric function is an incomplete beta function while the first can likely be simplified too. The first term is extracted avoiding division by $0$. Therefore:

$$\boxed{\int_0^\frac\pi4 x\tan^n(x)dx=\frac1{4n}\left(\frac1n\,_3\F_2(n,n,n;n+1,n+1;i)-\frac{i^n}n\,_3\F_2(n,n,n;n+1,n+1;-1)+\frac{\pi i}2\,_2\F_1(n,n;n+1;i)\right)+\sum_{k=1}^n\binom nk\frac{i^n(-1)^k}{4k}\left(\frac{i^k}k\,_3\F_2(k,k,n;k+1,k+1,-i)-\frac1k\,_3\F_2(k,k,n;k+1;k+1,-1)-\frac{\pi i^{k+1}}2\,_2\F_1(k,n;k+1;-i)\right)}$$

shown here:

to be simplified