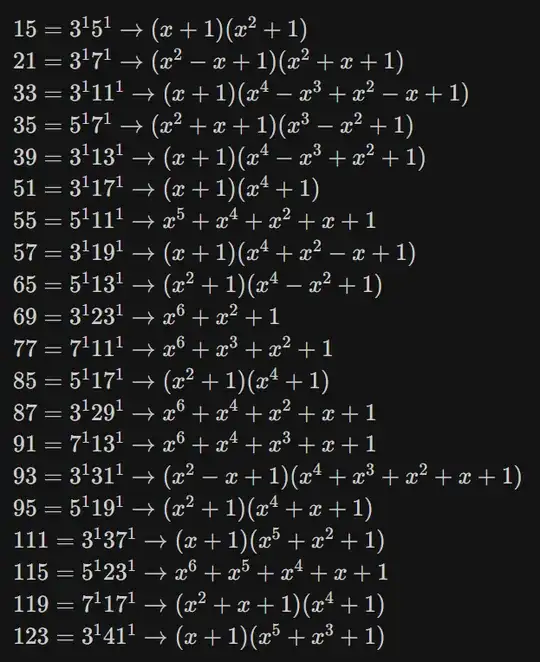For example, $x^2 - 1$ factors over $\mathbb{Z}[\sqrt{-1}]$.
I would like to ask if the polynomial $x^6 + x^2 + 1$ can be factored over an extension of $\mathbb{Z}$ by roots of unity.
EDIT: The community has requested I elaborate on what I've already tried.
I have tried many things, such as analyzing how the polynomial factors over $\mathbb{F}_p$, but nothing seems like it leads anywhere. The following is the motivation for the question:
The polynomial $x^6 + x^2 + 1$, evaluated at x = 2, returns $69 = 3 \times 23$. Performing this in the inverse for $3$ leads to $x + 1$, and for $23$ leads to $x^4 + x^2 + x + 1$, for coefficients in $\mathbb{Z}/2\mathbb{Z}$. Looking at the polynomial representation for binary representations of semiprimes, most of them seem to have some multiplicative-ish structure going on. For example, $21 = 3 \times 7$ leads to $(x^2 - x + 1)(x^2+x+1)$, which evaluate to 3 and 7 respectively at x = 2.
By asking the question, I wish to come across more intuition as to whether this multiplicative structure holds for extensions of $\mathbb{Z}$.
The given polynomial is among the first corresponding to an odd semiprime that does not factor in $\mathbb{Z}$:
While some of these factors include negative coefficients, to ensure uniqueness corresponding to the binary representation of $pq$, the full expansion of the polynomial enforced coefficients of $0$ or $1$.