13

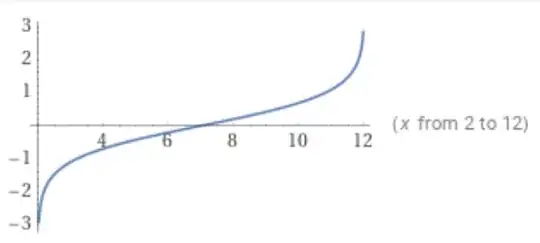
After some trial-and-error I've got this:

$$f(x;a,b)=\textrm{arctanh}\left( 2\frac{x-a}{b-a}-1 \right)$$

Illustrated here on WolframAlpha: arctanh((2*((x-a)/(b-a))-1)) where a=2 and b=12

arctanh((2*((x-a)/(b-a))-1)) where a=2 and b=12

It kind of does what I wanted, but I wonder if there are any functions like this that doesn't use trigonometric functions. Maybe something like an inverse general sigmoid function. I haven't been able to come up with anything like that.

André Christoffer Andersen
  • 335

3 Answers3

23

$\frac1 {a-x}+\frac 1 {b-x}$ is continuous and increasing on $(a,b)$ and its range is $(-\infty, \infty)$.

The derivative is $\frac 1 {(a-x)^{2}}+\frac 1 {(b-x)^{2}} >0$.

Kavi Rama Murthy
  • 359,332
  • 1
    @AndréChristofferAndersen the function geetha290km proposed, has $a-x$ in the first denominatior. Check this out: https://www.wolframalpha.com/input?i=1%2F%28a-x%29+%2B+1%2F%28b-x%29+where+a%3D2+and+b%3D12 – Veselin Dimov Aug 07 '23 at 07:51
  • 1
    @VeselinDimov Yes. Thanks. I noticed, and I tried to delete my comment in time, but you were too fast. I had a typo when I tested it out. This is a beautifully simple solution. – André Christoffer Andersen Aug 07 '23 at 07:54
9

Here's another one $$\ln \left( \left| \frac{x-a}{b-x} \right| \right)$$

Tony Mathew
  • 2,378
  • 6
  • 17
6

Let us follow your suggestion of finding something like an inverse general sigmoid function.

Start with the sigmoid expression $\frac{1}{1+e^{-y}}$.

We can scale the expression by $b-a$, and add $a$ to get an expression whose values lie in $(a,b)$. Then we can solve the equation

$x = a+\frac{b-a}{1+e^{-y}}$

for $y$ to find an expression for the inverse function. This gives us the expression

$y = -\ln(\frac{b-a}{x-a}-1) = \ln(\frac{x-a}{b-x})$,

which is the same answer as Tony Mathew gave.

Gunnar Sveinsson
  • 574
  • 3
  • 10
  • 2
    Interesting, you don't actually need to take the absolute. What I like about it, is that I am very familiar with manipulating sigmoid functions. I played around with doing what you did with the full generalized logistic function on Wikipedia and got this: https://www.wolframalpha.com/input?i=y+%3D+log%28-Q%2F%28C+-+%28%28A+-+K%29%2F%28A+-+x%29%29%5Ev%29%29%2FB+where+A%3D0%2C+K%3D1%2C+C%3D1%2C+Q%3D1%2C+B%3D1%2C+v%3D1 – André Christoffer Andersen Aug 07 '23 at 18:36
  • 1
    The reason you don't need to take the absolute is because $b - x > 0$ and $x - a > 0$ implicitly since our domain is $(a,b)$. – Gunnar Sveinsson Aug 07 '23 at 18:42
  • 1
    @AndréChristofferAndersen This is btw also essentially the same function as you came up with. Just scale your function by $1/2$. I think you might be confusing the inverse trigonometric function arctan with the inverse hyperbolic function arctanh (or artanh), as arctanh(x) is just $\frac{1}{2}\ln(\frac{1+x}{1-x})$. – Gunnar Sveinsson Aug 07 '23 at 18:45
  • 1
    That is so illuminating! Why didn't I bother to check? Here is my a=2 and b=12 example with the scaling you said. Fits like a glove: https://www.wolframalpha.com/input?i=plot+2arctanh%28%282%28%28x-2%29%2F%2812-2%29%29-1%29%29+and+ln%28%28x-2%29%2F%2812-x%29%29 – André Christoffer Andersen Aug 07 '23 at 18:58