Particularly nice bump function

Question

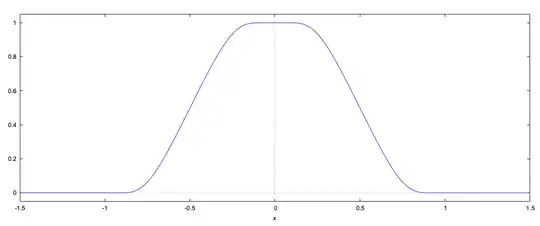
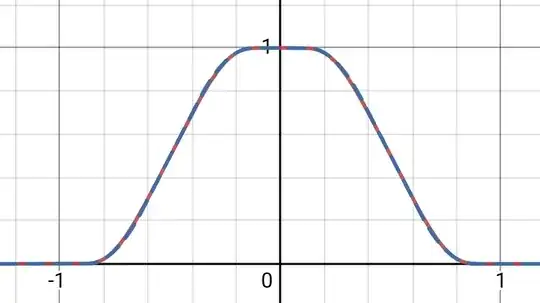
Is there a smooth ($C^\infty$) function $f: \mathbb{R} \to \left[ 0, 1 \right]$ such that:

• $f(x) = 1$ iff $x = 0$, $f(x) = 0$ iff $\left\lvert x \right\rvert \geq 1$, and $0 < f(x) < 1$ otherwise;
• Every derivative of $f$ is simultaneously $0$ at $x$ if and only if $x = 0$ or $\left\lvert x \right\rvert \geq 1$;
• $f(x) = f(-x)$ for all $x$;
• $f’(x) > 0$ for $-1 < x < 0$ and $f’(x) < 0$ for $0 < x < 1$; and
• $1 - f(x) = f(1 - x)$ for $0 \leq x \leq 1$?

If not, for which subsets of the above five conditions are there satisfactory functions? I know that the standard bump function $f(x) = e^{1 + 1/(x^2 - 1)}$ satisfies all but the last one of my conditions; what other conditions could I exclude, or is there an extension of one of the standard examples to meet the last criterion as well?

Answer 1

Similarly as in Bump function you can define $$ F(x)={\begin{cases}e^{-{\frac {1}{x}}}&{\text{if }}x>0,\\0&{\text{if }}x\leq 0,\end{cases}} $$ and $$ G(x)={\frac {F(1-x)}{F(x)+F(1-x)}},\qquad x\in \mathbb {R} . $$

$G$ has all desired properties on $[0, \infty)$ so that $$ f(x) = G(|x|) $$ has all five properties.

Plot created with wxMaxima:

F(x) := if x > 0 then exp(-1/x) else 0;
G(x) := F(1-x)/(F(x)+F(1-x));
wxplot2d(G(abs(x)), [x, -1.5, 1.5], same_xy);

Answer 2

A function that fulfill your requirements is the Rvachëv function $R(x)$, which is a displaced version of the first lobe of the Fabius function $F(x)$:

$$R(x)=\begin{cases} 0,\quad |x|\geq 1,\\ F(x+1),\ \text{otherwise}\end{cases}$$

It have some nice properties as fulfilling the Delayed differential equation: $$R'(x)=2\ R(2x+1)-2\ R(2x-1)$$ but also it have some "unfriendly properties" that make it unlikely to have a closed-form formula, since it inherit on $(-1,\ 1)$ the characteristics of the Fabius function, which is "an example of an infinitely differentiable function that is nowhere analytic".

In this answer it is shown a clever formula for approximate it through piecewise polynomials, but as a gross approximation it looks like pretty close to the function: $$f(x)=\begin{cases} 1,\quad x=0,\\ 0,\quad |x|\geq 1,\\ \dfrac{1}{1+\exp\left(\dfrac{1-2|x|}{x^2-|x|}\right)},\ \text{otherwise}\end{cases}$$ You could see both approximation here in Desmos

Added later: I think that $f(x)$ is equivalent to the answer given by @MartinR