Prime numbers as zeros of polynomials from the determinant of the form $P(x,N)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$

Question

Let $f(n)$ be some arbitrary sequence $\log(n),n,n^2,\dots$ $$f(n)=\log(n),n,n^2,\dots$$ and $$a(n)=\frac{\sum\limits_{d \mid n} f(d) \mu \left(\frac{n}{d}\right)}{\phi (n)}$$

and construct the polynomial $P(x,N)$ from the determinant:

$$P(x,N)=|x \gcd (n,k)-f(\gcd (n,k))|$$

$n=1,2,3,4,5,...N$
$k=1,2,3,4,5,...N$

It then appears

which is a $N$ by $N$ matrix starting:

$$\displaystyle P(x,N) = \left|\begin{array}{llllll} x-f(1) & x-f(1) & x-f(1) & x-f(1) & x-f(1) & x-f(1) & \cdots \\ x-f(1) & 2 x-f(2) & x-f(1) & 2 x-f(2) & x-f(1) & 2 x-f(2) & \cdots \\ x-f(1) & x-f(1) & 3 x-f(3) & x-f(1) & x-f(1) & 3 x-f(3) & \cdots \\ x-f(1) & 2 x-f(2) & x-f(1) & 4 x-f(4) & x-f(1) & 2 x-f(2) & \cdots \\ x-f(1) & x-f(1) & x-f(1) & x-f(1) & 5 x-f(5) & x-f(1) & \cdots \\ x-f(1) & 2 x-f(2) & 3 x-f(3) & 2 x-f(2) & x-f(1) & 6 x-f(6) & \cdots \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots \end{array}\right|$$

The first few polynomials, $N=1$, $N=2$ and $N=3$ are:

$$\begin{array}{l} x-f(1) \\ -f(2) x-f(1)^2+f(1) f(2)+x^2 \\ f(1) x^2-2 f(2) x^2-f(3) x^2-2 f(1)^2 x+f(1) f(2) x+f(2) f(3) x-f(1)^3+f(1)^2 f(2)+f(1)^2 f(3)-f(1) f(2) f(3)+2 x^3 \end{array}$$

Factoring the six first polynomials we get:

$$\begin{array}{l} x-f(1) \\ (x-f(1)) (f(1)-f(2)+x) \\ (x-f(1)) (f(1)-f(2)+x) (f(1)-f(3)+2 x) \\ (x-f(1)) (f(1)-f(2)+x) (f(1)-f(3)+2 x) (f(2)-f(4)+2 x) \\ (x-f(1)) (f(1)-f(2)+x) (f(1)-f(3)+2 x) (f(2)-f(4)+2 x) (f(1)-f(5)+4 x) \\ (x-f(1)) (f(1)-f(2)+x) (f(1)-f(3)+2 x) (f(2)-f(4)+2 x) (f(1)-f(5)+4 x) (-f(1)+f(2)+f(3)-f(6)+2 x) \end{array}$$

where a factored polynomial appears to be of the form:

$$\prod\limits_{n=1}^{n=N}\left(-\sum\limits_{d \mid n} f(d) \mu \left(\frac{n}{d}\right)+\phi (n)x\right) \tag{$\text{conjecture}$}$$

for square-free $n$ but not for $n=4$ which is a square, but I don't know for sure.

Solving for $x$: $$x_n = \frac{\sum\limits_{d \mid n} f(d) \mu \left(\frac{n}{d}\right)}{\phi (n)}$$ which means $$x_n=a(n)$$ since: $$a(n) = \frac{\sum\limits_{d \mid n} f(d) \mu \left(\frac{n}{d}\right)}{\phi (n)}$$

However, let: $$f(n)=n^2$$

and compute the polynomial roots of the above described determinant with the following Mathematica program:

(*start*)
Clear[a, f, n, k, nn, d, x];
nn = 100;
f[n_] := n^2
a[n_] := If[n < 1, 0, 
  Sum[f[d] MoebiusMu[n/d], {d, Divisors@n}]/
   EulerPhi[n]];
Table[a[n], {n, 1, nn}]
Monitor[x /. 
  Solve[Det[
     Table[Table[GCD[n, k]*x - f[GCD[n, k]], {k, 1, nn}], {n, 1, 
       nn}]] == 0, x], nn]
Sort[%%] - Sort[%]
(*end*)

Because the difference between the sorted values of $a(n)$ and $x_n$ in the last output is a vector of zeros we have numerically demonstrated that:

$$x_n=a(n)$$ for $$n=1,2,3,4,5,...N$$ when: $$N=100$$

So the for $100$ first terms of the Dedekind psi function A001615 the conjecture seems probable.

For $$f(n)=\log(n)$$ we appear to get $$x_n=\frac{\Lambda (n)}{\phi (n)}$$ as zeros of the polynomials:

$$P(x,N)=|x \gcd (n,k)-\phi (n)f(\gcd (n,k))|$$

or which is now the same:

$$P(x,N)=|x \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$

This Mathematica program computes $\Lambda (n)$ as zeros of those polynomials:

(*start*)
nnn = 9;
Monitor[Table[
  x /. Solve[
    Det[Table[
       Table[GCD[n, k]*x - EulerPhi[n]*Log[GCD[n, k]], {k, 1, 
         nn}], {n, 1, nn}]] == 0, x], {nn, 1, nnn}], nn]
TableForm[FullSimplify[%]]
(*end*)

but because of the logarithm function the program can only compute very slowly the $9$ first terms of the von Mangoldt function as polynomial zeros.

Now what happens if we take the logarithm of $x$ in

$$P(x,N)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$ $$?$$

With the following again very slow Mathematica program we can compute a few polynomial zeros:

(*start*)
Clear[n, k, nn, nnn, x];
nnn = 9;
Monitor[Table[
  x /. Solve[
    Det[Table[
       Table[GCD[n, k]*Log[x] - EulerPhi[n]*Log[GCD[n, k]], {k, 1, 
         nn}], {n, 1, nn}]] == 0, x], {nn, 1, nnn}], nn]
TableForm[FullSimplify[%]]
(*end*)

The result is a table:

$$\begin{array}{lllll} 1 & \text{} & \text{} & \text{} & \text{} \\ 1 & 2 & \text{} & \text{} & \text{} \\ 1 & 2 & 3 & \text{} & \text{} \\ 1 & 2 & 3 & \text{} & \text{} \\ 1 & 2 & 3 & 5 & \text{} \\ 1 & 2 & 3 & 5 & \text{} \\ 1 & 2 & 3 & 5 & 7 \\ 1 & 2 & 3 & 5 & 7 \\ 1 & 2 & 3 & 5 & 7 \end{array}$$

where the zeros at prime powers in the von Mangoldt function have dissappeared and the other polynomial roots $x_n$ have become whole numbers, starting like the prime numbers.

Letting $$N=80$$ and $x$ be a truncated vector of natural numbers: $$x=1,2,3,4,5...50$$ in the polynomial:

$$P(x,80)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$

in the following Mathematica program:

(*start*)
nn = 80
Chop[Table[
   Det[Table[
      Table[GCD[n, k]*Log[N[x, 12]] - EulerPhi[n]*Log[GCD[n, k]], {k, 
        1, nn}], {n, 1, nn}]]/Product[EulerPhi[m], {m, 1, nn}], {x, 1,
     50}]];
Flatten[Position[%, 0]]
(*end*)

we get:

{1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}

as polynomial roots of that determinant.

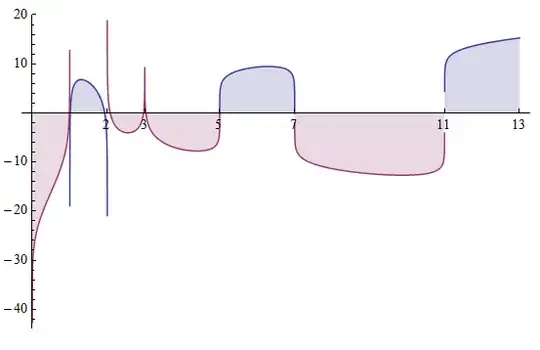
Plotting (the logarithm of) the $11$-th determinant polynomial of the form:

$$P(x,11)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$

(*start*)
nn = 11;
polynomial = 
  Det[Table[
    Table[GCD[n, k]*Log[x] - EulerPhi[k]*Log[GCD[n, k]], {k, 1, 
      nn}], {n, 1, nn}]];
Plot[{Log[polynomial], -Log[-polynomial]}, {x, 0, nn + 2}, 
 Filling -> Axis, Ticks -> {Prime[Range[nn + 2]]}]
(*end*)

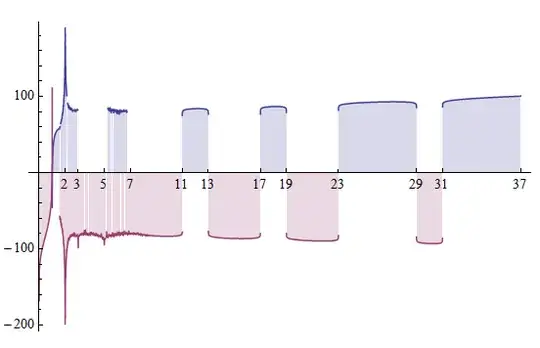
(*start*)
nn = 35;
polynomial = 
  Det[Table[
    Table[GCD[n, k]*Log[x] - N[EulerPhi[k], 80]*Log[GCD[n, k]], {k, 1,
       nn}], {n, 1, nn}]];
Plot[{Log[polynomial], -Log[-polynomial]}, {x, 0, nn + 2}, 
 Filling -> Axis, Ticks -> {Prime[Range[nn]]}]
N[polynomial]
(*end*)

Plotting the $35$-th determinant polynomial of the form:

$$P(x,35)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$

The numerical inaccuracies at the beginning of the plot are probably because the magnitude is very large $|\log(\text{plot})| \approx 100$.

Question:

Are the zeros of the polynomials

$$P(x,N)=|\log(x) \gcd (n,k)-\phi (n)\log(\gcd (n,k))|$$

equal to the set of prime numbers with $1$ included, for all integers $N$?