5

Problem: What is the limit $$\lim_{n\to\infty} n \sin (n! \cdot \pi \cdot e)$$

My work:

I expand $e$ by series, by using the same method from this old post:

$$ n!e=n!\cdot\sum_{k=0}^{+\infty}\frac{1}{k!}=A+\frac{1}{(n+1)}+\frac{1}{(n+1)(n+2)}+\cdots $$ where $A\in\mathbb{N}$. This gives the non-integer part:

$$ \{n! e\} = \frac{1}{n+1}+O\left(\frac{1}{n^2}\right)$$

Then I get the limit

$$\lim_{n\to\infty} n \sin (n! \cdot \pi \cdot e)=\lim_{n\to\infty} n \sin \left(\frac{\pi}{n+1}\right)=\pi$$

But I use Wolfram it says both the two limits are indeterminate, as shown below. Why is that?

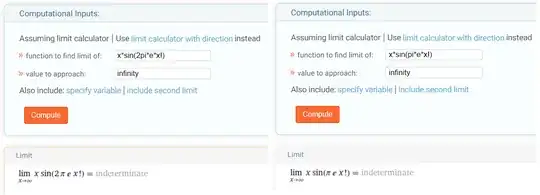
enter image description here

MathFail
  • 21,529
  • 2
    Note that $$ \sin (n! \mathrm{e}\pi ) = \sin (\left{ {n! \mathrm{e}} \right}\pi + \left\lfloor {n! \mathrm{e}} \right\rfloor \pi ) = ( - 1)^{\left\lfloor {n! \mathrm{e}} \right\rfloor } \sin (\left{ {n! \mathrm{e}} \right}\pi ) \ne \sin (\left{ {n! \mathrm{e}} \right}\pi ), $$ unless $\left\lfloor {n! \mathrm{e}} \right\rfloor$ is even which is not always the case. For the first limit, WA probably tries to compute the limit as $x\to+\infty$ through the reals and not just the integers. – Gary May 29 '23 at 07:29
  • 1
    You have calculated $\lim_{n\to\infty} |n \sin (n! \cdot \pi \cdot e)|$. – Koro May 29 '23 at 07:34
  • I see it now, thank you! –  May 29 '23 at 10:04

1 Answers1

6

Define $a_n=n\sin(n!\pi e)$. First, we do the Taylor series for $e$ $$e=1+1+\frac{1}2+\dots+\frac{1}{(n-2)!}+\frac{1}{(n-1)!}+\frac{1}{n!}+\frac{1}{(n+1)!}+\frac{e^c}{(n+2)!},~~~c\in (0,1)$$

we get

$$n!e=\underbrace{n!+n!+(3\cdot4\cdots n)+\cdots+(n-1)n}_{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=2m~\text{is an even integer}}+n+1+\frac{1}{n+1}+\frac{e^c}{(n+1)(n+2)}$$

Therefore,

$$\sin(n!\pi e)=\sin\left(2m\pi+ (n+1)\pi+\frac{\pi}{n+1}+\frac{e^c\pi}{(n+1)(n+2)}\right)$$ and

$$a_n=n\sin\left((n+1)\pi+\frac{\pi}{n+1}+\frac{e^c\pi}{(n+1)(n+2)}\right)$$

We compute the limit for subsequences $a_{2k}$ and $a_{2k-1}$:

$$\begin{align}\lim_{k\to\infty} a_{2k}&=-(2k)\sin\left(\frac{\pi}{2k+1}+\frac{e^c\pi}{(2k+1)(2k+2)}\right)=-\pi\\ \\ \lim_{k\to\infty} a_{2k-1}&=(2k-1)\sin\left(\frac{\pi}{2k}+\frac{e^c\pi}{(2k)(2k+1)}\right)=\pi\end{align}$$

So the limit does NOT exist.

Remarks:

For that old post, it is to evaluate $\lim n\sin(n!2\pi e)$, this is convergent, because after you do the same series expansion, you multiply $2\pi$ to the integer part, you get

$$\begin{align}\sin(n!2\pi e)&=\sin\left(4m\pi+ 2(n+1)\pi+\frac{2\pi}{n+1}+\frac{2e^c\pi}{(n+1)(n+2)}\right)\\ \\ &=\sin\left(\frac{2\pi}{n+1}+\frac{2e^c\pi}{(n+1)(n+2)}\right)\end{align}$$

so it won't split into two subsequences with $\pm$ sign issues.

MathFail
  • 21,529