I created a Sangaku-style geometry problem involving an equilateral triangle and three circles. Can you solve it without a computer?

Question

Inspired by this difficult Sangaku problem, I created the following Sangaku-style problem of my own.

In equilateral $\triangle ABC$, $D$ is on $AB$, $E$ is on $AC$, and the incircles of $\triangle ADE$, $\triangle DBE$ and $\triangle EBC$ are congruent. Prove that $BD=DE$.

I have a solution that requires a computer. I am looking for a solution that does not require a computer.

My solution

Assume the side length of $\triangle ABC$ is $1$.

Let
$x=BD$
$y=DE$
$\theta=\angle BDE$

Use the sine rule and cosine rule to express $\theta$, $AE$ and $BE$ in terms of $x$ and $y$:
$\theta=\arcsin{\left(\frac{\sqrt3 (1-x)}{2y}\right)}+\frac{\pi}{3}$
$AE=\sqrt{(1-x)^2+y^2+2y(1-x)\cos{\theta}}$
$BE=\sqrt{x^2+y^2-2xy\cos{\theta}}$

The inradius of a triangle is $\frac{2\times \text{area}}{\text{perimeter}}$.

$r_1=$ inradius of $\triangle ADE=\dfrac{y(1-x)\sin{\theta}}{1-x+y+AE}$

$r_2=$ inradius of $\triangle DBE=\dfrac{xy\sin{\theta}}{x+y+BE}$

$r_3=$ inradius of $\triangle EBC=\dfrac{(1-AE)\frac{\sqrt3}{2}}{2-AE+BE}$

Setting $r_1=r_2$ and $r_1=r_3$ gives two equations in $x$ and $y$. Desmos shows they are satisfied only when $x=y$, both approximately $0.5502282106$.

Answer 1

Here is a solution from one of my coworkers.

Assume $AD=DE$ and $OF=KG=r$. We will prove that $HL=r$.

Define $\alpha=\angle{DAE}$. Simple angle chasing gives the other angles shown in the diagram.

$$AT=CO+OE+EK$$ $$\frac1r(OE+CO)=\frac1r(AT-EK)$$ $$\cot{(60^0-\alpha)}+\sqrt3=\cot{\left(30^0-\frac{\alpha}{2}\right)}-\cot{\left(30^0+\frac{\alpha}{2}\right)}$$ $$\frac{\cos{\alpha+\sqrt3 \sin{\alpha}}}{\sqrt3 \cos{\alpha}-\sin{\alpha}}+\sqrt3=\frac{\sin{(30^0+\alpha/2)\cos{(30^0-\alpha/2)-\cos{(30^0+\alpha/2)}\sin{(30^0-\alpha/2)}}}}{\sin{(30^0-\alpha/2)\sin{(30^0+\alpha/2)}}}$$ $$\frac{\cos{\alpha}+\sqrt3 \sin{\alpha}}{\sqrt3\cos{\alpha}-\sin{\alpha}}+\sqrt3=\frac{2\sin{\alpha}}{\cos{\alpha}-\cos{60^0}}$$ $$2\cos^2{\alpha}-\cos{\alpha}=\sqrt3 \sin{\alpha}\cos{\alpha}-\sin^2{\alpha}$$ $$\cos^2{\alpha}-\cos{\alpha}+1=\sqrt3\sin{\alpha}\cos{\alpha}$$ $$(\cos^2{\alpha}-\cos{\alpha}+1)^2=3(1-\cos^2{\alpha})\cos^2{\alpha}$$ $$(2\cos{\alpha}-1)(2\cos^3{\alpha}-1)=0$$ Obviously, $\cos{\alpha}\ne1/2$.

Let $m=2^{1/3}$.

$$\cos{\alpha}=\frac1m=\frac{1-\tan^2{(\alpha/2)}}{1+\tan^2{(\alpha/2)}}$$ $$\tan{\alpha}=\sqrt{m^2-1}$$ $$\tan{\frac{\alpha}{2}}=\sqrt{\frac{m-1}{m+1}}$$ $$\begin{align} HL&=DE\cos{\alpha}\tan{\frac{\alpha}{2}}\\ &=(DM+ME)\cos{\alpha}\tan{\frac{\alpha}{2}}\\ &=r(\cot{\alpha}+\cot{(60^0-\alpha)})\cos\alpha\tan{\frac{\alpha}{2}}\\ &=r\left(\frac{1}{\sqrt{m^2-1}}+\frac{1+\sqrt3\sqrt{m^2-1}}{\sqrt3-\sqrt{m^2-1}}\right)\frac1m\sqrt{\frac{m-1}{m+1}}\\ &=\frac{\sqrt3mr}{(m+1)(\sqrt3-\sqrt{m^2-1})}\\ &=\frac{\sqrt3mr}{\sqrt3m+\sqrt3-(m+1)\sqrt{m^2-1}}\\ &=\frac{\sqrt3mr}{\sqrt3m+\sqrt3-\sqrt{\color{red}{(m^2-1)(m+1)^2}}}\end{align}$$

$$\color{red}{(m^2-1)(m+1)^2}=(m+2)(m^3-2)+3=0+3=3$$

$$\therefore HL=r$$

Answer 2

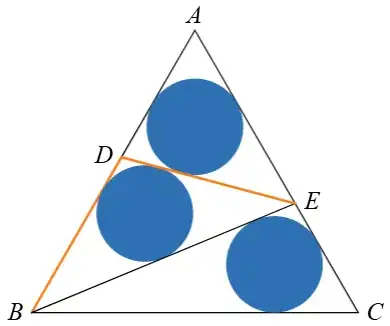
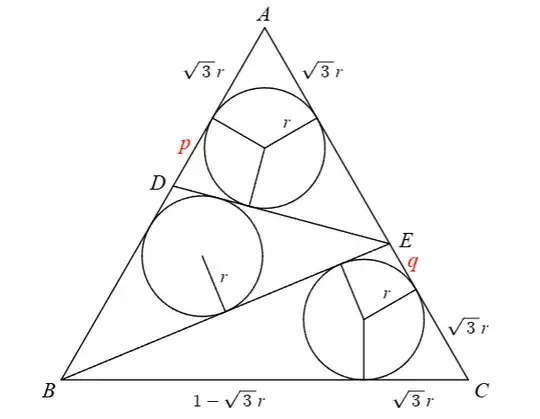
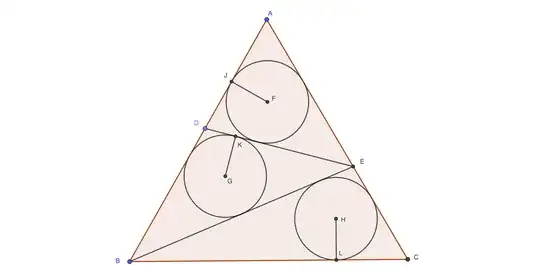
I uh, wasted so much time on this. I have no idea if there is a shorter solution, all data pieces are seemingly used by the time we get to $\left ( 2 \right )$. I'm not defining every point, refer to the figure. Circles $X$,$Y$, and $Z$ just refer to the circles which have those points as their center.

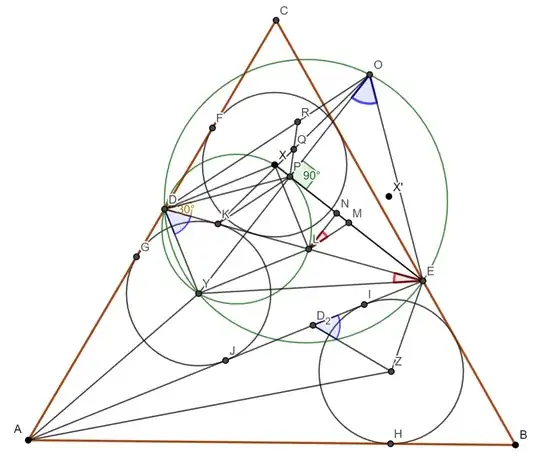
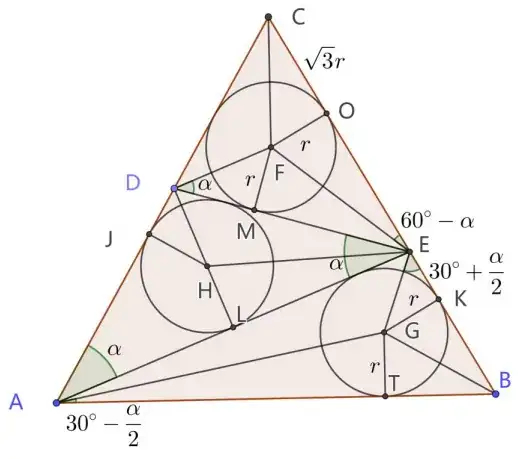
Rotate $\triangle YDX$ $180^{\circ}$ around the midpoint of $XY$ to get $\triangle XLD$. Clearly the midpoint of $XY$ lies on $DE$ because circles $X$ and $Y$ have the same radius and are both tangent to $DE$. Furthermore we have $YDX=90^{\circ}$ since $DY$ bisects $\angle ADE$ and $DX$ bisects $\angle EDC$. This implies $YDXL$ is a rectangle, so $DL=YX$. $YGFX$ is also a rectangle so $YX=GF$.

Since $\angle ACB =\angle CBA$ and circles $X$ and $Z$ have equal radius, $CF=BH$. Then $AC=AB \implies AF=AH$ and $AH=AI$, since both segments are tangent to circle $Z$ passing through $A$. This implies $GF=JI$ and $DL=JI$. We have $EJ=EK \implies DL+IE=KL+LE \implies DK+IE=LE$. Let $D_2$ lie between $IJ$ with $D_2I=DX$.

You can show that for any triangle $\triangle ABC$, $2 \cdot \angle BIC=180^{\circ}+\angle BAC$, where $I$ is the incenter of $\triangle ABC$. Call this Lemma 1. This means $\angle DXE=120^{\circ}$, so $\angle LXE=30^{\circ}$.

$IZ=KY \implies DY=D_2Z$ and $XL=D_2Z$. Let $X'$ form a parallelogram $XLEX'$. we have $X'EL=XLD=YDL$, $X'E=XL=DY=D_2Z$, and $LE=D_2E$, which means $LEX' \cong ED_2Z$. This means $LX'=EZ$, and since $XLEX'$ is a parallelogram, the midpoint $M$ of $LX'$ lies on $EX$ and we will have $LM=\frac{EZ}{2}$ and $\angle ELM=\angle IEZ$.

$\angle MLX=180^{\circ}-\angle XLD-\angle ELM=180^{\circ}-\angle YDL-\angle IEZ=180^{\circ}-(\angle XCE+\angle CEX)-\angle IEZ=90^{\circ}-30^{\circ}+(90^{\circ}-\angle CEX-\angle IEZ)=60^{\circ}+\angle KEY$

(We have three pairs of equal angles around $E$, so the sum of one from each pair will be $90^{\circ}$). Now drop a perpendicular from $L$ onto $XE$ and label the intersection $N$. $\angle LXE=30^{\circ} \implies \angle NLX=60^{\circ}$, $NL=\frac{XL}{2}$, and $\angle MLN=\angle KEY$. This means $\triangle MLN \sim \triangle YEK$, and we have $\frac{NL}{LM}=\frac{KE}{EY} \implies \frac{\frac{DY}{2}}{\frac{EZ}{2}}=\frac{KE}{EY} \implies \frac{DY}{EZ}=\frac{KE}{EY} \left ( 2 \right )$.

Construct $O$: $\triangle YEO \sim \triangle EZD_2$. Then from $\left ( 2 \right )$, $\frac{OE}{EY}=\frac{D_2Z}{EZ}=\frac{KE}{EY} \implies OE=KE$. $\angle OEY=\angle EZD_2=\angle MLX=60^{\circ}+\angle KEY \implies OEK=60^{\circ}$. Note that also $\angle YOE=\angle YDE$, so $YDOE$ is cyclic.

The next construction is not very instructive or enlightening but works regardless. Just a lot of trial and error. Let $P$ be the foot of the perpendicular from $E$ onto $YO$. We already established $\angle XEY+\angle IEZ=90^{\circ}$, so $P$ lies on $EX$. This gives $\angle XPY=90^{\circ} \implies YDXPL$ is cyclic $\implies \angle DPY=\angle DLY$. Using Lemma 1, $\angle AYE=90^{\circ}+\angle YDE \implies \angle DPY+\angle AYE=180^{\circ} \implies \angle OPD=\angle AYE$. Combined with the fact that $\angle DOY=\angle DEY$ as $YDOE$ is cyclic, $\triangle DPO \sim \triangle AYE$ (Incidentally, $\triangle DKO \sim \triangle EZA$). We also get $\angle LDP=\angle LXP = 30^{\circ}$.

Next, $YKPE$ is cyclic since $\angle KYE=\angle YPE=90^{\circ}$ degrees, so $\angle EYP=\angle EKP$, i.e. $KP \| DO$. We are almost done, let $Q$ be the midpoint of $KO$. $KE=OE \implies \angle EQO=90^{\circ}$ and $\angle OEQ=\frac{60^{\circ}}{2}=30^{\circ}$. This means $EPQO $ is cyclic, so $\angle OPQ=30^{\circ}$. Let $R$ be the intersection of $PQ$ with $DO$. $KP \| DO \implies QPK \sim QRO$. As $KQ=QO$ we also have $KP=RO$. This means $KROP$ is a parallelogram, so $\angle KRP=\angle RPO=30^{\circ}$, so $KDRP$ is cyclic, which means $\angle PRO=180^{\circ}-\angle DRP=\angle PKD$, which means $PRO \sim DKP$. But $KP=RO$, so $DP=PO$, so $AY=YE$ and we are done. (It means $\angle EAY=\angle YEA \implies \angle EAD=\angle DEA \implies AE=AD$)

This doesn't appear generalizable, at least with the current proof: we use $AB=AC$ right at the start, a 30-60-90 triangle to establish $\left ( 2 \right )$, not to mention $2\angle KDP=\angle OEK$.

Using $AD=DE$, it's not too bad to show that $EX=EB$, but I want to be done with this.

Answer 3

Here is a proof from one of my high school students.

---

Assume the side lengths of $\triangle ABC$ are $1$.

Let $r=$ radius of the three inscribed circles.

Label lengths $p$ and $q$ as shown in the diagram.

We will use two formulas for the area of a triangle:

• $\text{Area}=\frac12ab\sin C$ for general triangle $ABC$
• $\text{Area}=\frac12(\text{radius of incircle})(\text{perimeter of triangle})$. This follows from dividing the triangle into three smaller triangles by drawing line segments from the incenter to each vertex, and adding the areas of the three smaller triangles.

First:

$$\color{blue}{\text{Area}_{\triangle BCE}}=\frac12(BC)(CE)\sin C=\frac12r(BC+CE+BE)$$

$$\frac12(1)(q+\sqrt3r)\frac{\sqrt3}{2}=\frac12r(1+(q+\sqrt3r)+(1-\sqrt3r+q))$$

$$\frac12(1)(q+\sqrt3r)\frac{\sqrt3}{2}=\color{blue}{\frac12r(2+2q)}$$

$$\therefore\color{red}{q=\frac{r}{\sqrt3-4r}}$$

Then:

$$AC=1$$

$$AE+q+\sqrt3r=1$$

$$AE=1-q-\sqrt3r$$

$$\therefore\color{red}{AE=\frac{4\sqrt3r^2-8r+\sqrt3}{\sqrt3-4r}}$$

Then:

$$\color{green}{\text{Area}_{\triangle ADE}}=\frac12(AD)(AE)\sin B=\frac12r(AD+AE+DE)$$

$$\frac12(p+\sqrt3r)(AE)\frac{\sqrt3}{2}=\frac12r((p+\sqrt3r)+AE+(p+AE-\sqrt3r))$$

$$\frac12(p+\sqrt3r)(AE)\frac{\sqrt3}{2}=\color{green}{\frac12r(2p+2AE)}$$

$$p=\frac{(AE)r}{\sqrt3(AE-4r)}$$

$$\therefore\color{red}{p=\frac{4\sqrt3r^3-8r^2+\sqrt3r}{28r^2-12\sqrt3r+3}}$$

Then:

$$\text{Area}_{\triangle BED}=\text{Area}_{\triangle ABC}-\color{blue}{\text{Area}_{\triangle BCE}}-\color{green}{\text{Area}_{\triangle ADE}}=\frac12r(BE+DE+BD)$$

$$\frac{\sqrt3}{4}-\color{blue}{\frac12r(2+2q)}-\color{green}{\frac12r(2p+2AE)}=\frac12r((1-\sqrt3r+q)+(p+AE-\sqrt3r)+(1-p-\sqrt3r))$$

Using our previous expressions for $\color{red}{q,AE,p}$ in terms of $\color{red}{r}$, this becomes:

$$320\sqrt3r^4-792r^3+228\sqrt3r^2-78r+3\sqrt3=0$$

(Sanity check: this equation is satisfied by the value of $r$ from @Blue's comment to the OP, i.e. $r= \frac{\sqrt{3}}{30}\left(7 - \sqrt[3]{2} - 2 \sqrt[3]{4}\right) = 0.148106\ldots$.)

Factorize:

$$(8r-\sqrt3)(40\sqrt3r^3-84r^2+18\sqrt3r-3)=0$$

We know that $r$ cannot equal $\frac{\sqrt3}{8}$, because this is larger than $\frac{\sqrt3-1}{4}$, which is the largest possible radius of three congruent non-overlapping circles inscribed in $\triangle ABC$.

$$\therefore 40\sqrt3r^3-84r^2+18\sqrt3r-3=0$$

This can be rearranged as:

$$\frac{80\sqrt3r^4-280r^3+112\sqrt3r^2-54r+3\sqrt3}{-112r^3+76\sqrt3r^2-48r+3\sqrt3}=1$$

$$2\left(\frac{4\sqrt3r^3-8r^2+\sqrt3r}{28r^2-12\sqrt3r+3}\right)+\frac{4\sqrt3r^2-8r+\sqrt3}{\sqrt3-4r}=1$$

$$2p+AE=1$$

$$1-p-\sqrt3r=p+AE-\sqrt3r$$

$$\therefore BD=DE$$

Answer 4

The following does not use a computer, except for GeoGebra, and argues not from equal inradii to $BD=DE$, but rather the converse: if $BDE$ is a certain constructible isosceles triangle, then the inradii are equal.

In equilateral triangle $ABC$, with side $AB=1$, construct $\angle CBE=22.5^o$ and $\angle AED=45^o$. Since $\angle BEC=180^o-60^o-22.5^o=97.5^o$, then $\angle DEB=\angle EBD=37.5^o$ and $BD=DE=x$ in triangle $BDE$.

Since the inradius is twice the area divided by the perimeter, in triangle $ADE$,$$FJ=\frac{x(1-x)\sin 75^o}{x+(1-x)+AE}$$Relying on GeoGebra, that $x\approx\frac {11}{20}=.55$, then by the law of cosines$$AE=\sqrt{x^2+(1-x)^2-2x(1-x)\cos75^o}\approx .614$$and$$FJ\approx\frac{.239}{1.614}=.148$$ Next, in triangle $DBE$, since $\angle BDE=105^o$, then $$GK=\frac{x\sin 37.5^o\cdot BE}{2x+BE}$$and$$BE=\sqrt {2x^2-2x^2\cos 105^o}\approx.873$$so that$$GK\approx\frac{.292}{1.973}=.148$$Finally, in triangle BEC, again$$HL=\frac{BC\cdot BE\sin 22.5^o}{BE+EC+BC}=\frac{.873\cdot\sin 22.5^o}{.873+(1-.614)+1}\approx\frac{.334}{2.259}=.148$$Thus it seems possible, with ruler and compass, in an equilateral triangle to construct three triangles, the middle one isosceles, such that their incircles are equal.

Triangle $ADE$ is oddly reminiscent of the first Pythagorean triple, having its angles rather than its sides in the $3-4-5$ ratio. Moreover, all angles are integral multiples of $7.5^o$, as indicated in the figure below.

Answer 5

Here is a response to OP's Bonus Question.

Let $ABC$ be a $30^o-60^o-90^o$ right triangle. Construct $DE$ perpendicular bisector of $AB$, and join $EB$.

Since, by SAS, $\triangle ADE\cong\triangle DBE$, then$$\frac{FH}{GI}=\frac{\triangle ADE}{\triangle DBE}=\frac{AE+ED+DA}{BE+ED+DB}=\frac{1}{1}$$[More briefly: Congruent triangles have equal incircles.]

Next, since $\angle EBD=\angle DAE=30^o$, then $\angle CBE=\angle EBD$, and by AAS, $\triangle DBE\cong\triangle CBE$, and again$$\frac{GI}{JK}=\frac{\triangle DBE}{\triangle EBC}=\frac{BE+ED+DB}{BE+EC+CB}=\frac{1}{1}$$

Therefore, a $30^o-60^o-90^o$ right triangle is divisible into three equal triangles having equal inradii, and$$\frac{AB}{BC}=\frac {2}{1}$$Is this the only triangle to fulfill the conditions? It seems clear that since equal triangles under the same height must have equal bases, then triangles $ADE$, $DBE$ will have equal perimeters, making $FH=GI$, only if $ED\perp AB$ so that $AE=BE$.

Likewise, equal triangles $DBE$, $CBE$ on the same base $BE$ have equal perimeters, making $GI=JK$, only if the triangles are congruent (if two equal triangles on the same base are non-congruent, the more nearly isosceles triangle has a greater incircle), i.e. only if $\angle ECB=\angle BDE=90^o$, and hence $\angle CBA=2\angle EBA$. Therefore, since $\angle CBA+\angle CAB=90^o$, then $\angle CBA=60^o$ and $\angle CAB=30^o$.

Finally, and by the way, as in the solution for equilateral $ABC$, here too we find $\angle AED=2\angle CBE$.