1

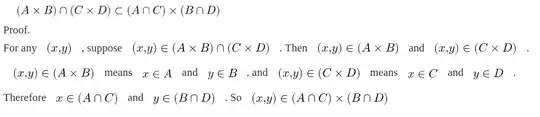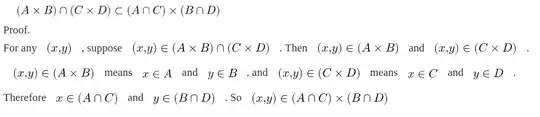
enter image description here

To prove that for every $x$, $(x\in Z\implies x\in R),$ is it ok to write "For any $x,$ suppose $x\in Z$. Then... Then $x\in R$" ?

For example, in the above proof of $$\forall x{,}y\left(\left(\left(x{,}y\right)\in\left(A\times B\right)\cap\left(C\times D\right)\right)\rightarrow\left(\left(x{,}y\right)\in\left(A\cap C\right)\times\left(B\cap D\right)\right)\right),$$ is the way that I introduce $(x,y)$ valid? Or does my wording mean $\forall x{,}y\left(\left(x{,}y\right)\in\left(A\times B\right)\cap\left(C\times D\right)\right)$ ? This would mean that all $(x,y)$ are elements of $\left(A\times B\right)\cap \left(C\times D\right)$, which is false.

Would it be better to say: "Consider any $\left(x{,}y\right)\in \left(A\times B\right)\cap \left(C\times D\right)$" ?

ryang
  • 44,428
lightyourassonfire
  • 355
  • I would simply remove "For $(x,y)$," at the biginning. The phrase "Suppose $(x,y)\in\dots$" already introduced the $(x,y)$. You do not need to be that formal. You are not writing a formal proof anyway. – Paprika7191 May 25 '23 at 17:32
  • @durianice ok, then when i conclude that the other is a subset, do i need to say that "Since $(x,y)$ was arbitrary.." – lightyourassonfire May 25 '23 at 17:34
  • It actually very much depends on your audience and your intention. Normally, you won't need to add that $(x,y)$ is arbitrary because everyone understands it. If you want to be absolutely clear, add that. – Paprika7191 May 25 '23 at 17:36
  • Your largest technical hiccup is that you started with $(x,y)$. It would need to start "Let $z \in (A\times B) \cap (C \times D)$. – Brian Moehring May 25 '23 at 17:44
  • @BrianMoehring what do you mean? That i need to use $z$ instead of $(x,y)$? Or that i need to introduce the variable with "let"? This post says to not use "let" for universal quantification: https://matheducators.stackexchange.com/questions/17952/can-we-avoid-confusion-over-using-let-as-a-quantifier/18155#18155 – lightyourassonfire May 25 '23 at 17:50
  • As for my point, it was about the use of $z$ to denote an arbitrary element of the set rather than only showing it for particular elements of a certain type (in the formal proof, we can't leverage intuition about the form of the elements) – Brian Moehring May 25 '23 at 17:58
  • @BrianMoehring From the book "how to prove it": "In most proofs involving Cartesian products mathematicians suppress this step. If it is clear from the beginning that an object will turn out to be an ordered pair, it is usually just called (x, y) from the outset." – lightyourassonfire May 25 '23 at 18:39
  • You have chosen a strange position. Mathematicians generally write for mathematicians, so of course they skip details that are simple. In contrast though, if a mathematician came up to me and said "You shouldn't use a bare 'let'," when the conversation wasn't about pedagogy, then I'd mentally label them a pedant and ignore them. – Brian Moehring May 25 '23 at 19:04
  • @BrianMoehring "of course they skip details that are simple", then why did you say that i would need to start with $z$ and not $(x,y)$ – lightyourassonfire May 25 '23 at 19:16
  • I have assumed you aren't writing this proof in order to convince a mathematician of the truth of the statement. If you are writing it as a student (for instance, to show your proficiency), then we would need to see that you understand the technical aspects of the proof. – Brian Moehring May 25 '23 at 19:20

2 Answers2

1

Your proof is fine.

For a slightly more precise wording I would recommend starting with

Let $(x,y)\in ...$

and then proceeding exactly as you have.

NOTE

Despite some of the comments about "let", this is used throughout algebra texts:-

Let $G$ be a finite group ...

Let $p$ be an odd prime ...

and so on.

This is always used to mean "Let * be any ...".

user1172706
  • 2,791
  • i just read a post about not using "let" for universal quantification: https://matheducators.stackexchange.com/questions/17952/can-we-avoid-confusion-over-using-let-as-a-quantifier/18155#18155 – lightyourassonfire May 25 '23 at 17:39
  • Not when I was being trained! The author of that article was happy with "Let $(x,y)$ be any element of ... " which is the meaning of the symbols I used. – user1172706 May 25 '23 at 17:43
  • 1
    @lightyourassonfire While it may be true there's an pedagogical reason to avoid using "let" in the classroom due to students' misunderstanding it, its use in mathematics is non-controversial. Specifically, it's used not to specify a particular type of instantiation but rather to introduce a new non-logical symbol. That's it. Any other interpretation people might assign to it just comes from the fact we often compound the introduction of a non-logical symbol with a corresponding logical statement. – Brian Moehring May 25 '23 at 20:26
0

enter image description here

Do you mean that I need to introduce the variable with "let"? I just read a post about not using "let" for universal quantification.

The word "let" merely assigns meaning and does not in itself connote universal quantification. In any case, even though your opening clause "for any $(x,y)$" is ostensibly suggesting universal quantification, technically at this point in the proof you're merely dealing with an arbitrary $(x,y);$ this is indicated by the phrase "any $(x,y)$".

As such, you might as well just spell it out instead: "Let $(x,y)$ be arbitrary. Suppose that..." (the first sentence can be omitted and left tacit).

Alternatively, rewrite the opening sentence as "Let $(x,y)$ be any element of $\left(A\times B\right)\cap \left(C\times D\right)$".

Would it be better to say: "Consider any $\left(x{,}y\right)\in \left(A\times B\right)\cap \left(C\times D\right)$" ?

Sure, this is good too.

Is the way that I introduce $(x,y)$ valid? Or does my wording mean $\forall x{,}y\left(\left(x{,}y\right)\in\left(A\times B\right)\cap\left(C\times D\right)\right)$ ?

No, your opening sentence is not asserting that every $(x,y)$ belongs to that set intersection: it is merely introducing a couple then making a supposition—not an assertion—about it. The substance of your proof is fine.

When I conclude, do I need to say: "Since $(x,y)$ was arbitrary.." ?

Only if you wish to summarise your proof and explicitly display the theorem statement. This step can also be omitted and left tacit, depending on your preferred level of detail.

Addendum

Suppose that for any x, x∈Z means ∀x x∈Z, right ?

No: ∀x x∈Z means for each x, x∈Z (no "suppose that"), while suppose that for any x, x∈Z is not really an assertion/statement (the phrase "suppose that" roughly means "if").

On the other hand, suppose that for any x, x∈Z; then P is true is symbolised either as (∀x x∈Z) ⟹ P or (∃x x∈Z) ⟹ P, depending on the context: Translating 'any' as ∀ or ∃.

ryang
  • 44,428