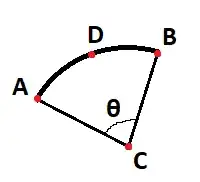
For an arc in 3D space with the following known variables:
- $A$: start point
- $B$: end point
- $C$: center point
- $r$: radius
- vector normal to the surface of the arc
How can we calculate the coordinates of the point $D$ lying in the middle of the arc using the swept angle $\fracθ2$? How would this angle be calculated correctly?
I have tried the following:
- Calculate the $X$ direction vector as $X = C - A$.
- Calculate the Y direction vector as Y = normal x X.
- Get the vectors from center to start and end, $CA$ and $CB$ respectively.
- Calculate swept angle as $\theta = \arccos\left(\frac{CA\cdot{CB}}{{\lvert CA\rvert}{\lvert CB\rvert}}\right)$.
- $D = C + X_{dir}\cdot{r}\cdot{\cos{\frac{\theta}{2}}}+ Y_{dir}\cdot{r}\cdot{\sin{\frac{\theta}{2}}}$
This way I am sometimes getting a diametrically opposite point. The problem seems to be that the sign of the angle $\theta$ I am calculating does not respect the direction of the normal axis.