This question may be too vague for the MSE crowd, if so, please feel free to ask clarifying questions or just remove.
The Chebyshev polynomials are a family of orthogonal polynomials typically defined over the domain $x\in[-1,1]$. The nth Chebyshev polynomial of the first kind takes the form: $$ T_n(x) = \cos(n \arccos(x)) = \frac{1}{2}((x-(\sqrt{x^2-1})^n+(x+\sqrt{x^2-1})^n)) $$
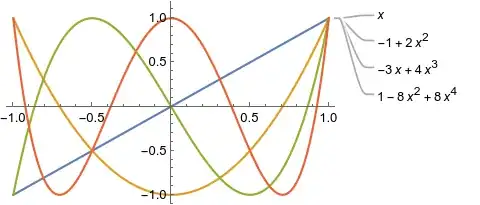
For reference, here's a plot of the first 4 Chebyshev polynomials of the first kind:
The Chebyshev polynomials have an interesting geometric interpretation as well, namely they are the projection of the cosine/sine functions defined on a cylinder onto a bisecting plane.
So I had this thought, what if I treated the cylinder as a Riemann surface and stereographically projected the cylinder it onto the whole real line?
Doing a little math, one finds that this encoding induces the following change of variables:
$$ x\mapsto \frac{x}{\sqrt{x^2+1}} $$
And carrying out this transformation in the definitions of the Chebyshev polynomials, one finds:
$$ \tilde{T_n}(x) = \frac{1}{2\sqrt{1+x^2}^n}((x-i)^n+(x+i)^n)\\ =\frac{1}{2}\bigg(\bigg(\frac{x-i}{x+i}\bigg)^{n/2} + \bigg(\frac{x+i}{x-i}\bigg)^{n/2}\bigg) $$
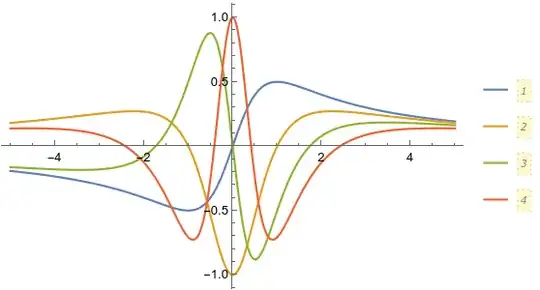
Which, when plotted look like:
Interesting features:
The zeros of the standard Chebyshev polynomials have roots that concentrate near the boundary [-1,1], these polynomials have roots that will actually concentrate near the origin.
One can deal with problems in an unbounded domain, by instead studying a problem in the unit interval.
Main questions:
Are these transformed polynomials related to any already known orthogonal polynomials?
Has this transformation been studied before, if so, what is known about them?
Has this been "useful" in solving any particular problem?
 $T_n(x)$" />
$T_n(x)$" />