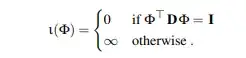0

While reading the following paper on an optimization problem, there was a variant of an orthogonal Procrustes problem, where the solution is an element of the Stiefel manifold. The authors provided a closed-form solution, but I couldn't understand how they derived it!

Given $Y$ is an $n \times k$ matrix and $D$ is an $n \times n$ diagonal matrix of strictly positive values on its main diagonal, the following optimization problem in $n \times k$ matrix $\Psi$

$$ {\bf \Psi}^{*} = \arg\min_{{\bf \Psi}, {\bf \Psi}^{\top}{\bf \Psi} = {\bf I}} \left\Vert {\bf D}^{-\frac12} {\bf \Psi} - {\bf Y} \right\Vert_2^2 $$

The $\left\Vert\cdot\right\Vert_2$ refers to the Frobenius norm, and the solution they used is as follows:

$$ {\bf \Psi}^{*} = \bf{Y}\bf{V}\bf{W}^{-\frac12}\bf{V}^{\top} $$

where $\bf{V}$, $\bf{W}$ and $\bf{V}^{\top}$ are obtained via the SVD decomposition

$$ (\bf{D}^{\frac{1}{2}}\bf{Y})^{\top}(\bf{D}^{\frac{1}{2}}\bf{Y}) = \bf{V}\bf{W}\bf{V}^{\top} $$

I attached the screenshot of the problem from the paper (we want to solve equation 10, the equations of interest are 14, 15 and 16), any help is appreciated!

enter image description here

enter image description here

schlodinger
  • 101
  • Please clarify in what sense this is a variant of the orthogonal Procrustes problem. – Rodrigo de Azevedo Feb 05 '23 at 11:18
  • If the Frobenius norm were used – Rodrigo de Azevedo Feb 05 '23 at 13:53
  • 2
    Looking at the paper, this norm is being used in ADMM in the penalty term. It doesn't appear to matter whether you use the 2-norm or Frobenius norm for that purpose (they're topologically equivalent norms.) It's quite common in my experience for machine learning folks to write 2-norm when they mean the Frobenius norm. – Brian Borchers Feb 05 '23 at 16:10
  • So, if it's Frobenius norm, how to solve this problem, I looked at the thread you sent @RodrigodeAzevedo but I can't see how they derived the solution in equation 16 – schlodinger Feb 05 '23 at 17:44
  • The transformation of (10) into (14) requires this to be the Frobenius norm. – Brian Borchers Feb 05 '23 at 18:48
  • Note that $\min | D^{-1/2} \Psi - Y |{F}^{2} $ is equivalent to minimizing the Frobenius norm squared of the transpose, $\min | \Psi^{T} D^{-T/2} -Y^{T} |{F}^{2}$. – Brian Borchers Feb 05 '23 at 18:53
  • @BrianBorchers Do we know how to solve $\left\Vert \bf{\Psi}^{\top}(\bf{D}^{\frac{-1}{2}})^{\top} - \bf{Y}^{\top} \right\Vert_F^2$ under the condition of being in the Stiefel manifold in closed form? – schlodinger Feb 06 '23 at 03:18
  • I don't know how to do it, and I'm not convinced the paper is correct in the solution it gives, but a quick google scholar search reveals some papers on this variation on the procrustes problem. – Brian Borchers Feb 06 '23 at 04:39

0 Answers0