3

I am specifically interested in implementing animations for Cellular Automata in the Hyperbolic Plane. I have seen Coordinate systems for the hyperbolic plane on Wikipedia, but a lot of what Professor Margenstern mentions in his Cellular Automata in Hyperbolic Spaces research regarding coordinates is not mentioned in that wiki page (I don't think).

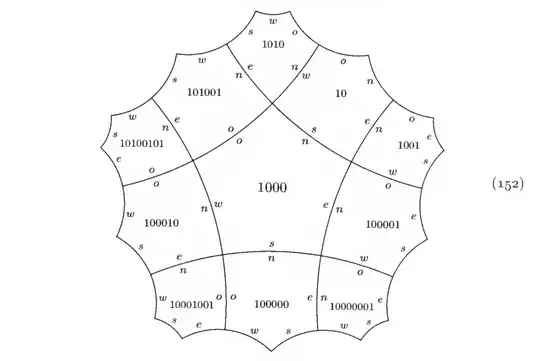
In Volume 1 of his books, he mentions Fibonacci Trees as a way of constructing/indexing 2 hyperbolic tessellations, the pentagrid {5,4} and heptagrid {7,3}, but I don't think others. In About a new splitting for the algorithmic study of the tilings {p,q} of the hyperbolic plane when q is odd, he describes "spanning trees" for the case where q is odd and also when q is even, which I think could be used for coordinates but I'm not an expert.

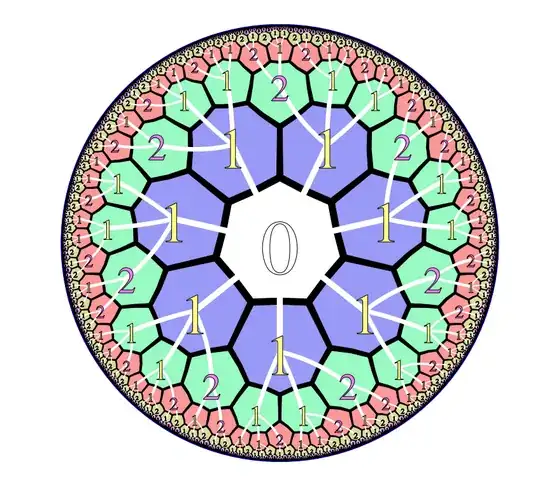
What do we have in terms of coordinate systems which are based on the underlying tiling data, not on the literal geometric projection pixels/angles? I am looking for a coordinate system that is independent of pixels/physical positions, and instead relies upon position of the polygons relative to vertices/edges on another polygon, relative to some base/central polygon. Perhaps some sort of tree data, I don't know enough yet. What is the standard coordinate system taking these factors into account?

I'm imagining something like this:

enter image description here

These HyperRogue notes were also helpful.

Donald Knuth referenced Margenstern's work in Art of Computer Programming 4A, but only in regards to the pentagrid:

enter image description here

Lance Pollard
  • 3,915
  • Your usage of the word "coordinates" seems nonstandard: Given that you are ruling out "geometric projection pixels/angles", I take it that you are also ruling out numerical coordinates such as the Poincaré disc model and various associated formulas? Assuming those things are indeed ruled out, some kind of positive description of what you would rule in would be helpful in understanding what you are asking. – Lee Mosher Jan 23 '23 at 22:14
  • @LeeMosher I don't know if I am ruling out the numerical coordinates of the Poincaré disc model, I know about the disk model, but don't know what coordinate system you are referring to. I am looking for some sort of binary-encoded mapping or integer-encoded system like what Knuth was trying to do for the Pentagrid (just added above). Something that looks at a path and the turns you can make with edges/vertices, something like that. – Lance Pollard Jan 23 '23 at 22:24
  • Here is an example coordinate system for one tessellation. – Lance Pollard Jan 24 '23 at 01:21
  • 1
    See also my answer to Symbolic coordinates for a hyperbolic grid. You might want to provide details whether you only want to label individual cells, or also positions within cells. – MvG Jan 25 '23 at 20:36

0 Answers0