The solid angle can be expressed in terms of complete elliptic integrals of first and third kind.
I believe this is first derived by F. Paxton in 1959.
THE REVIEW OF SCIENTIFIC INSTRUMENTS. VOLUME 30, NUMBER 4 APRIL, 1959.
Solid Angle Calculation for a Circular Disk. F. PAXTON
A copy of the article can be found
here.
Below is my attempt to derive the same result in an alternate manner.
The integral is indeed trickier than I thought.
To avoid confusion with the usage of $x,y,z$ as coordinates, let us change the problem and assume the circular disk $C$ we are dealing with lies in the plane $z = b$, centered at $(a,0,b)$ with radius $s$. We will assume $a, b > 0$ and $a \ne s$.
In terms of ordinary spherical polar coordinates $(r,\theta,\phi)$, points on the plane $z = b$ can be parametrized as:
$$(x,y,z) = (b\tan\theta \cos\phi,\,b\tan\theta\sin\phi,\, b)$$
Let $\rho = \sqrt{x^2+y^2} = b\tan\theta$, the "element" for integrating the solid angle is given by:
$$d\Omega
= \sin\theta d\theta \wedge d\phi
=\frac{\tan\theta d\tan\theta}{\sqrt{1 + \tan\theta^2}^3} \wedge d\phi
= \frac{b \rho d\rho \wedge d\phi}{\sqrt{\rho^2+b^2}^3}
= \frac{b\;dx \wedge dy}{\sqrt{\rho^2+b^2}^3}
$$
Introduce complex coorindates $\eta = x + iy$ and $\bar{\eta} = x - iy$, the solid angle
extended by $C$ can be rewritten as:
$$\begin{align}
\Omega_{C}
= & \int_{C} d\Omega
= \frac{b}{2i}\int_{C} \frac{d\bar{\eta} \wedge d\eta}{\sqrt{\eta\bar{\eta}+b^2}^3}
=\color{blue}{^{[1]}} \frac{b}{i} \int_C d\left(\frac{1}{\eta}\left( \frac{1}{b} - \frac{1}{\sqrt{\eta\bar{\eta}+b^2}}\right)\right) \wedge d\eta\\
= & \frac{b}{i} \int_{\partial C} \left(\frac{1}{b} - \frac{1}{\sqrt{\eta\bar{\eta} + b^2}}\right) \frac{d\eta}{\eta}
= 2\pi \delta_{C} + ib \int_{\partial C} \frac{d\eta}{\eta \sqrt{\eta\bar{\eta} + b^2}}
\end{align}$$
where $\delta_{C} = 1 \text{ or } 0$ depends on whether $s > a$ or $< a$. In other words, whether $\partial C$ contains $0$ or not.
On $\partial C$, we can parametrize $\eta$ as $s e^{it} + a$ and $\bar{\eta}$ as $s e^{-it} + a$. Substitute this into above expression, we obtain:
$$\begin{align}
&\Omega_C - 2\pi \delta_{C}\\
= &ib \int_{-\pi}^{\pi} \frac{ dt }{\sqrt{ s^2 + a^2 + b^2 + 2sa\cos t}}\frac{ is e^{it}}{s e^{it} + a }\\
= & -b
\int_{0}^{\pi} \frac{ dt }{\sqrt{ s^2 + a^2 + b^2 + 2sa\cos t}}
\left( \frac{s e^{it}}{s e^{it} + a } + \frac{s e^{-it}}{s e^{-it} + a } \right)\\
= & -b
\int_{0}^{\pi} \frac{ dt }{\sqrt{ s^2 + a^2 + b^2 + 2sa\cos t}}
\frac{2s(s + a\cos t)}{s^2 + a^2 + 2sa\cos t}\\
= & -b
\int_{0}^{\pi} \frac{ dt }{\sqrt{ s^2 + a^2 + b^2 + 2sa\cos t}}
\left( 1 + \frac{s^2 - a^2}{s^2 + a^2 + 2sa\cos t} \right)\\
= & -2b
\int_{0}^{\pi/2} \frac{ dt }{\sqrt{ s^2 + a^2 + b^2 + 2sa\cos(2t)}}
\left( 1 + \frac{s^2 - a^2}{s^2 + a^2 + 2sa\cos(2t)} \right)\\
= & -2b
\int_{0}^{\pi/2} \frac{ dt }{\sqrt{ (s+a)^2 + b^2 - 4sa\sin^2(t)}}
\left( 1 + \frac{s^2 - a^2}{(s+a)^2 - 4sa\sin^2(t)} \right)
\end{align}$$
The last integral can be expressed in terms of the
complete elliptic integral
of first and third kind:
$$
K(k) = \int_{0}^{\frac{\pi}{2}} \frac{dt}{\sqrt{1-k^2\sin^{2}t}}
\quad\text{ and }\quad
\Pi(n,k) = \int_{0}^{\frac{\pi}{2}} \frac{dt}{(1-n\sin^{2}t)\sqrt{1-k^2\sin^{2}t}}
$$
The final results are:
$$\Omega_{C} = 2\pi\delta_C -\frac{2b}{\sqrt{(s+a)^2+b^2}}
\left(\;K(k) + \left(\frac{s-a}{s+a}\right) \Pi(n,k)\;\right)
$$
where $\displaystyle \;\;k = \sqrt{\frac{4sa}{(s+a)^2+b^2}}
\quad\text{ and }\quad
n = \frac{4sa}{(s+a)^2}
$.
Notes
$\color{blue}{[1]}$ When $C$ contains $(0,0,b)$, we need the $\frac{1}{b}$ term. It regularize the 1-form at $\eta = 0$ and make Stroke's theorem continue to work.
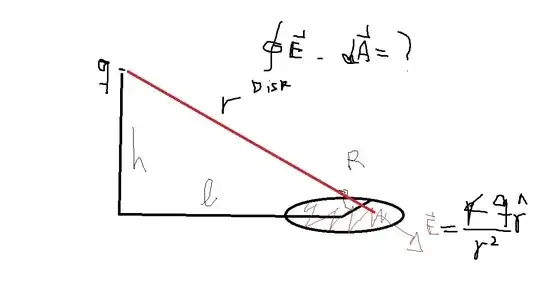If we have a point charge at the origin and we want to find the flux through a disk of radius $R$ which is located at $(x,0,z)$ and lies parallel to the $x-y$ plane we will have to do a tricky integral. We can write down the exact $E.dA$ or we can try and find the solid angle (turns out it is like finding the flux through an ellipse at $(0,0,z)$).
