17

Take the list of primes, $$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, \ldots$$ and create ordered $(x,y)$ pairs by grouping in sequence, $$(2, 3), (5, 7), (11, 13), (17, 19), (23, 29), (31, 37), (41, 43), (47, 53), (59, 61), (67, 71), \ldots$$ and now plot these points:


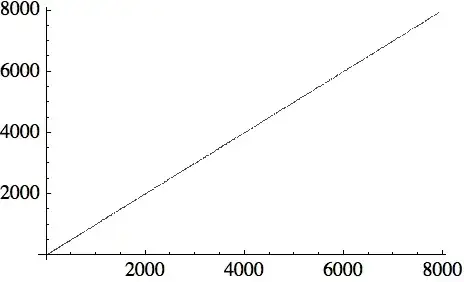
   PrimePairs1000
The best-fit slope for the first $10^3$ primes (shown) is $1.00046$; for the first $10^5$ primes, the slope is $1.0000024$. Why such rapid and close approach to a slope of $1$? I (naively) expected more variation/spread...

What property of an increasing list of numbers would ensure this pairing will closely approach a slope of $1$?

Joseph O'Rourke
  • 31,079
  • 4
    The distance from a prime $p$ to the next prime is, on average, about $\log p$, and, conjecturally, never much more that $(\log p)^2$; these are tiny, compared to $p$ (for large $p$). I suspect you'd get similar behavior for $(n^2,(n+1)^2)$, though maybe not converging as fast. – Gerry Myerson Aug 04 '13 at 00:57
  • 1
    Thank you, Gerry & Will! It is a vivid demonstration of just how small is $\log p$. – Joseph O'Rourke Aug 04 '13 at 01:52

1 Answers1

11

It is really just that prime gaps remain quite small. If $q$ is the next prime larger than $p,$ then for all known primes, $$ q < p + 3 \log^2 p. $$ This is currently unprovable but consistent with Cramer's conjecture. All that can be proved is something like $q < p + p^{0.55}$ for sufficiently large $p,$ i don't think there is even a known bound for beginning of that behavior. So proof is far behind observation.

Here is a nice table of prime gaps. Since the merit is the gap over $\log p,$ all one needs to do to get the gap divided by $\log^2 p$ is divide by another $\log p.$ They tell you the number of digits in each P, and then $\log P$ is about 2.3 times $\log_{10} P.$ It would be nice HINT HINT to see this big table with each gap divided by $\log^2 p,$ as Guy does below.

Richard K. Guy, in Unsolved Problems in Number Theory, gives the gaps divided by $\log^2 p.$ In the second edition (1994), page 21, in the third edition (2004), page 36.

enter image description here

 Stolen from 
 http://users.cybercity.dk/~dsl522332/math/primegaps/maximal.htm

 the size of the gap is g

 next are the number of decimal digits in p

 for 4 * 10^18 > p >= 11, g < log^2 p = (log p)^2.

 Oh, logarithms base e == 2.718281828459


 ==================================
          g   digits of p             p    log p   g/log p  g/log^2 p
   1      1   1                        2 0.693147   1.4427    2.08137
   2      2   1                        3  1.09861  1.82048    1.65707
   3      4   1                        7  1.94591  2.05559    1.05637
   4      6   2                       23  3.13549  1.91357   0.610294
   5      8   2                       89  4.48864  1.78228   0.397065
   6     14   3                      113  4.72739  2.96147   0.626449
   7     18   3                      523  6.25958  2.87559    0.45939
   8     20   3                      887  6.78784  2.94644   0.434076
   9     22   4                     1129  7.02909  3.12985   0.445271
  10     34   4                     1327  7.19068  4.72835   0.657566
  11     36   4                     9551   9.1644  3.92824   0.428642
  12     44   5                    15683  9.66033  4.55471   0.471486
  13     52   5                    19609  9.88374  5.26116   0.532305
  14     72   5                    31397  10.3545  6.95352   0.671548
  15     86   6                   155921  11.9571  7.19238   0.601515
  16     96   6                   360653  12.7957  7.50254   0.586334
  17    112   6                   370261   12.822  8.73501   0.681254
  18    114   6                   492113  13.1065    8.698   0.663642
  19    118   7                  1349533  14.1153  8.35974   0.592248
  20    132   7                  1357201  14.1209  9.34782   0.661983
  21    148   7                  2010733   14.514   10.197   0.702566
  22    154   7                  4652353  15.3529  10.0307   0.653342
  23    180   8                 17051707  16.6518  10.8097   0.649161
  24    210   8                 20831323   16.852  12.4615   0.739466
  25    220   8                 47326693  17.6726  12.4487   0.704405
  26    222   9                122164747  18.6209  11.9221   0.640254
  27    234   9                189695659  19.0609  12.2764   0.644062
  28    248   9                191912783  19.0726   13.003   0.681764
  29    250   9                387096133  19.7742  12.6427   0.639356
  30    282   9                436273009  19.8938  14.1753   0.712549
  31    288  10               1294268491  20.9812  13.7266   0.654231
  32    292  10               1453168141   21.097  13.8408   0.656056
  33    320  10               2300942549  21.5566  14.8447   0.688637
  34    336  10               3842610773  22.0694  15.2247   0.689855
  35    354  10               4302407359  22.1824  15.9586   0.719423
  36    382  11              10726904659   23.096  16.5396   0.716125
  37    384  11              20678048297  23.7523  16.1668   0.680642
  38    394  11              22367084959  23.8309  16.5332   0.693772
  39    456  11              25056082087  23.9444  19.0441   0.795349
  40    464  11              42652618343  24.4764  18.9571   0.774506
  41    468  12             127976334671  25.5751   18.299   0.715502
  42    474  12             182226896239  25.9285   18.281   0.705055
  43    486  12             241160624143  26.2087  18.5434   0.707529
  44    490  12             297501075799  26.4187  18.5475   0.702059
  45    500  12             303371455241  26.4382   18.912   0.715328
  46    514  12             304599508537  26.4423  19.4386   0.735133
  47    516  12             416608695821  26.7554  19.2858   0.720819
  48    532  12             461690510011  26.8582  19.8078   0.737495
  49    534  12             614487453523  27.1441  19.6728   0.724756
  50    540  12             738832927927  27.3283  19.7597   0.723048
  51    582  13            1346294310749  27.9284   20.839   0.746159
  52    588  13            1408695493609  27.9737  21.0198   0.751412
  53    602  13            1968188556461  28.3081   21.266   0.751232
  54    652  13            2614941710599  28.5923  22.8034   0.797536
  55    674  13            7177162611713  29.6019  22.7688   0.769166
  56    716  14           13829048559701  30.2578  23.6633   0.782057
  57    766  14           19581334192423  30.6056  25.0281   0.817762
  58    778  14           42842283925351  31.3885  24.7861   0.789655
  59    804  14           90874329411493  32.1405  25.0152   0.778307
  60    806  15          171231342420521   32.774  24.5926   0.750369
  61    906  15          218209405436543  33.0165  27.4408   0.831126
  62    916  16         1189459969825483  34.7123  26.3884   0.760203
  63    924  16         1686994940955803  35.0617  26.3535   0.751632
  64   1132  16         1693182318746371  35.0654  32.2825   0.920639
  65   1184  17        43841547845541059  38.3194  30.8982   0.806335
  66   1198  17        55350776431903243  38.5525  31.0745   0.806032
  67   1220  17        80873624627234849  38.9317   31.337   0.804922
  68   1224  18       203986478517455989  39.8568  30.7099   0.770506
  69   1248  18       218034721194214273  39.9234  31.2598   0.782995
  70   1272  18       305405826521087869  40.2604  31.5943   0.784749
  71   1328  18       352521223451364323  40.4039  32.8681   0.813489
  72   1356  18       401429925999153707  40.5338  33.4536   0.825325
  73   1370  18       418032645936712127  40.5743  33.7652   0.832181
  74   1442  18       804212830686677669  41.2286  34.9757   0.848335
  75   1476  19      1425172824437699411  41.8008  35.3103   0.844728
        g   digits of p             p    log p   g/log p  g/log^2 p
 ==================================
joriki
  • 242,601
Will Jagy
  • 146,052