Random uniform points on the surface of (hyper) ellipsoid

Question

How to generate random uniform points on (hyper) ellipsoid?

Note: Rejection methods are very inefficient specially in higher dimension. Check the ratio of volumes (box VS its inscripted ellipsoid) as the dimension grows.

Note 2: Here's an elegant way of generating uniform distribution on a sphere, using a Gaussian vector. I guess I need do modify the norm to obtain a uniform distribution on an ellipsoid.

import numpy as np
import matplotlib.pylab as plt
fig = plt.figure(figsize=(7, 7))
ax = fig.add_subplot(projection='3d')
dim = 3
x = np.random.normal(0,1,(1100,dim))
z = np.linalg.norm(x, axis=1) 
z = z.reshape(-1,1).repeat(x.shape[1], axis=1) 
y = x/z * 1 * np.sqrt(dim)
ax.scatter(y[:,0], y[:,1], y[:,2]);

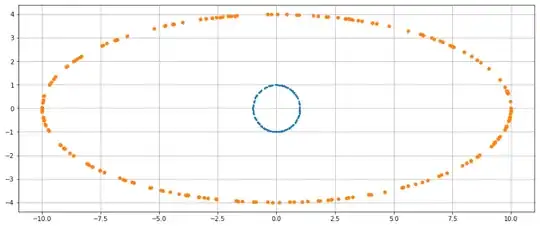
Update : The results with Cholesky factor decomposition.

dim = 2 # test in 2D
r=1
A = np.array([[1/10**2, 0],
               [0, 1/4**2]])
L = np.linalg.cholesky(A).T
x = np.random.normal(0,1,(200,dim))
z = np.linalg.norm(x, axis=1)  dimension
z = z.reshape(-1,1).repeat(x.shape[1], axis=1) 
y = x/z * r #uniform points on a sphere
y_new = np.linalg.inv(L) @ y.T # expected transformation
plt.figure(figsize=(5,5))
plt.plot(y[:,0],y[:,1], linestyle="", marker='o', markersize=2)
plt.plot(y_new.T[:,0],y_new.T[:,1], linestyle="", marker='o', markersize=5)
plt.gca().set_aspect(1)
plt.grid()

Answer 1

If the ellipsoid is defined as the set of vectors $x$ satisfying $x'Ax = r^2$ then:

• take the upper triangular Cholesky factor of $A$, say $U$;
• sample $y$ uniformly on the sphere with radius $r$;
• take $x = U^{-1}y$.

I don't remember why it works. This is the way used in my R package uniformly and I certainly found this method by googling.

---

EDIT: this method is wrong

Here is a R code for a working method:

runifonellipsoid <- function(n, A, r) {
  S <- A / (r * r)
  stopifnot(isSymmetric(S))
  e <- eigen(S, symmetric = TRUE)
  if(any(e$values <= 0)) stop("`S` is not positive.")
  radiisq <- 1 / e$values # squared radii of the ellipsoid
  radii <- sqrt(radiisq)
  rot <- e$vectors # rotation between ellipsoid and its axes-aligned version
  # simulations
  xyz <- t(vapply(radii, function(r) {
    rnorm(n, 0, r)
  }, FUN.VALUE = numeric(n))) 
  d <- sqrt(colSums(xyz*xyz / radiisq))
  sims0 <- t(xyz) / d
  # rotate
  t(rot %*% t(sims0))
}