We wish to compute
$$
\int_{-\infty}^\infty\frac{\mathrm{d}x}{(e^x-x)^2+\pi^2}\tag{1}
$$
We will do so by computing the contour integral
$$
\int_{\gamma_R}\frac{\mathrm{d}z}{(e^z-z)^2+\pi^2}\tag{2}
$$
over a family of contours $\gamma_R$ for suitable values of $R$.
The Singularities
The singularities of the integrand in $(2)$ occur when $(e^z-z)^2+\pi^2=(e^z-z+\pi i)(e^z-z-\pi i)$ vanishes; that is, for $z_k^\pm=x_k^\pm+iy_k^\pm$ where
$$
e^{z_k^\pm}-z_k^\pm\pm\pi i=0\tag{3}
$$
that is
$$
e^{2x_k^\pm}={x_k^\pm}^2+(y_k^\pm\mp\pi)^2\tag{4}
$$
and
$$
y_k^\pm=\mathrm{atan2}(y_k^\pm\mp\pi,x_k^\pm)\tag{5}
$$
In fact, the roots of $(3)$ can be expressed in terms of the multivalued Lambert W function as
$$
z_k^\pm=-W_{-k}(1)\pm\pi i\tag{6}
$$
The negative indices ensure that $z_0^+$ and $z_k^\pm$ for $k>0$ are in the upper half-plane. In Mathematica, these can be computed as -LambertW[-k,1]+Pi I and -LambertW[-k,1]-Pi I.
Note that as $|z_k^\pm|\to\infty$, $(3)$ precludes $x_k^\pm$ from being negative. In fact, as specified in $(6)$, only $x_0^\pm<0$. Equation $(4)$ says that
$$
|y_k^\pm\mp\pi|=\sqrt{e^{2x_k^\pm}-{x_k^\pm}^2}\tag{7}
$$
As $|z_k^\pm|\to\infty$, $(5)$ and $(7)$ yield
$$
|y_k^\pm|\to\frac\pi2\pmod{2\pi}\tag{8}
$$
The Contours
We will use the contours, $\gamma_R=\overline{\gamma}_R\cup\overset{\frown}{\gamma}_R$, which circle the upper half plane, $\overline{\gamma}_R$ passing from $-R$ to $R$ on the real axis, then $\overset{\frown}{\gamma}_R$ circling back counter-clockwise along $|z|=R$ in the upper half-plane. To get the desired decay of the integral along $\overset{\frown}{\gamma}_R$, we will also require that $R\equiv\frac{3\pi}{2}\!\!\!\!\pmod{2\pi}$; this is so that $\overset{\frown}{\gamma}_R$ passes well between the singularities.
Let us also define the curves $\rho^\pm$ to be where $|e^z|=|z\mp\pi i|$. Note that all the singularities of the integrand in $(2)$ lie on $\rho^\pm$.
On $\rho^\pm$, we have $R-\pi\le e^x\le R+\pi$, therefore,
$$
\log(R-\pi)\le x\le\log(R+\pi)\tag{9}
$$
Furthermore, because $R-|y|=\frac{x^2}{R+|y|}<\frac{\log(R+\pi)^2}{R}$, we have
$$
R-\frac{\log(R+\pi)^2}{R}\le|y|\le R\tag{10}\\
$$
Therefore, at $\overset{\frown}{\gamma}_R\cap\rho^\pm$ as $R\to\infty$,
$$
\text{on }\overset{\frown}{\gamma}_R\text{, }x^2+y^2=R^2\Rightarrow\left|\frac{\mathrm{d}y}{\mathrm{d}x}\right|=\left|\frac xy\right|\sim\frac{\log(R)}{R}\to0
$$
and
$$
\text{on }\rho^\pm\text{, }e^{2x}=x^2+(y\mp\pi)^2\Rightarrow\left|\frac{\mathrm{d}y}{\mathrm{d}x}\right|=\left|\frac{e^{2x}-x}{y\mp\pi}\right|\sim R\to\infty
$$
Thus, at $\overset{\frown}{\gamma}_R\cap\rho^\pm$ as $R\to\infty$, $\overset{\frown}{\gamma}_R$ becomes horizontal and $\rho^\pm$ becomes vertical. For example, here is the situation when $R=129.5\pi$:
$\hspace{35mm}$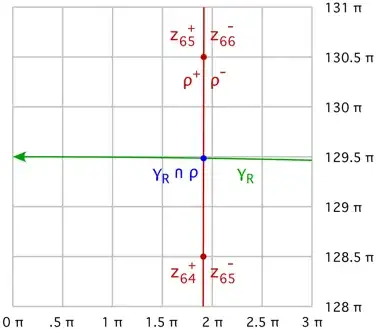
$$
\hspace{-1cm}\small
\begin{array}{}
z_{64}^+=5.99292081954932666 + 403.67969492855003099 i\\
z_{65}^-=6.00848352082933166 + 403.67988772309602824 i\\
z_{65}^+=6.00848352082933166 + 409.96307303027561472 i\\
z_{66}^-=6.02380774554030566 + 409.96326053797959857 i
\end{array}
$$
As $R\to\infty$, on $\rho^\pm$ in the upper half-plane, $(9)$ and $(10)$ imply that $\arg(z\mp\pi i)\to\frac\pi2$; thus, as indicated by $(8)$, $e^z$ and $z\mp\pi i$ cancel only when $\mathrm{Im}(z)\approx\frac\pi2\!\!\!\!\pmod{2\pi}$. Likewise, $e^z$ and $z\mp\pi i$ reinforce when $\mathrm{Im}(z)\approx\frac{3\pi}{2}\!\!\!\!\pmod{2\pi}$.
Therefore, when $R\equiv\frac{3\pi}{2}\!\!\!\!\pmod{2\pi}$ and $z\in\overset{\frown}{\gamma}_R\cap\rho^\pm$, we have that $|e^z-z\pm\pi i|\sim2R$. As $z\in\overset{\frown}{\gamma}_R$ moves to the right, by even just $1$, $e^z$ more than doubles, and dominates $z\mp\pi i$; thus, $|e^z-z\pm\pi i|\ge2R-R$. As $z\in\overset{\frown}{\gamma}_R$ moves to the left, by even just $1$, $e^z$ decreases by more than half, and $z\mp\pi i$ dominates; thus, $|e^z-z\pm\pi i|\ge R-R/2$. Therefore, when $R\equiv\frac{3\pi}{2}\!\!\!\!\pmod{2\pi}$, $|e^z-z\pm\pi i|\ge R/2$, and $|(e^z-z)^2+\pi^2|\ge R^2/4$. This guarantees that, as $R\to\infty$, the integral over $\overset{\frown}{\gamma}_R$ vanishes.
Thus, the integral along the real axis is $2\pi i$ times the sum of the residues in the upper half-plane.
The Residues
Let $z_k^\pm=-W_{-k}(1)\pm\pi i$. We will use the fact that $e^{z_k^\pm}-z_k^\pm=\mp\pi i$.
The residue of $\displaystyle\frac1{(e^z-z)^2+\pi^2}$ at $z_k^\pm=-W_{-k}(1)\pm\pi i$ is
$$
\begin{align}
\lim_{z\to z_k^\pm}\frac{z-z_k^\pm}{(e^z-z)^2+\pi^2}
&=\frac1{2(\mp\pi i)(e^{z_k^\pm}-1)}\\
&=\frac1{2\pi i}\frac1{\mp(z_k^\pm-1\mp\pi i)}\\
&=\frac1{2\pi i}\frac1{\pm(W_{-k}(1)+1)}\\
\end{align}
$$
Thus, the residues at the pairs of singularities cancel each other, leaving us with the residue at $z_0^+$ which is $\dfrac1{2\pi i}\dfrac1{W_0(1)+1}$. Thus, the integral is
$$
\int_{-\infty}^\infty\frac{\mathrm{d}x}{(e^x-x)^2+\pi^2}=\frac1{W_0(1)+1}
$$
