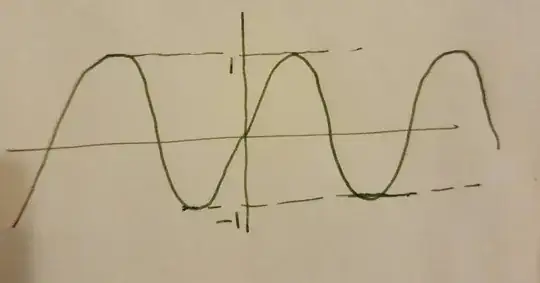
I was thinking about a ODE problem recently when I was reading about dynamical system. In school we used to solve the ODE problem $\frac{dx}{dt}=\sqrt{1-x^2}, x=0, t=0$ as $x=\sin(t),$ which will have the graph
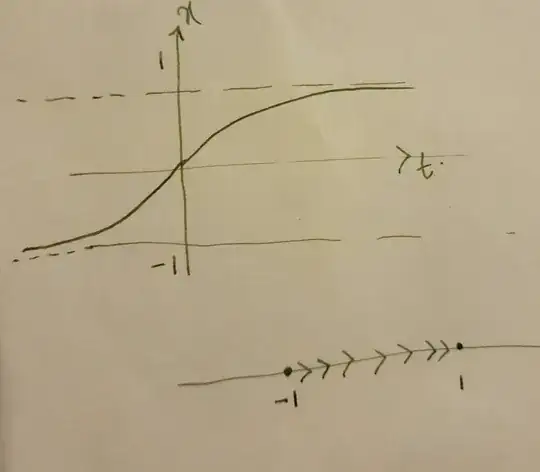
Now in dynamical system we can see that the fixed points are $\pm 1$ so specifically we can observe if the solution hits $1$ or $-1$ it should not increase or decrease from there. Specifically if we draw the phase diagram we can conclude that the solution passing through $(0,0)$ should look like
and it seems reasonable. So I am surprised that we were taught wrong for many days. Isn't it? Or, am I making any mistake?