I think it's worth expanding my initial observations into a full answer. But first, let me temper some expectations. The Collatz iterates are famously complex, and stopping times are known to be quite erratic. There isn't a whole lot that is known about them, other than probabilistic/asymptotic arguments. There is much that is understood, so a clear, big picture, penny-drop moment might well be off the table, at least for now. It's possible that a passing person might come up with some incredible insight, but the chances are extremely low.
Generating pairs of equivalent stopping times
Let $T$ be the Collatz iteration function and suppose we have a number of the form $k + 2^am$, where $a \ge 1$, and $m$ is odd. $T$ behaves predictably on this number. In particular,
$$T(k + 2^am) = \cases{3k+1 + 2^a(3m) & \text{if $k$ is odd} \\ \frac{k}{2} + 2^{a-1}m & \text{if $k$ is even.}}$$
Or, in other words, $T(k + 2^am) = T(k) + 2^{a'}m'$, where $a'$ and $m'$ are either $a$ and $3m$, or $a-1$ and $m$, depending on whether $k$ was odd or even.
We can keep track of the iterates this way, for as long as we have $a \ge 1$; after this, it won't be clear whether the number is odd or even. Basically, we get exactly $a$ even steps before we have to give this up.
Now, if we know that the iterates for two numbers $k_1 + 2^am$ and $k_2 + 2^am$ meet before $a$ even steps are performed (i.e. they both come to a number of the form $k_3 + 2^{a'}m'$ for some $a'$ and $m'$) but after the same number of total iterations, then we know that $k_1 + 2^am$ and $k_2 + 2^am$ have the same stopping time.
Finding such relations will produce infinitely many pairs (or possibly even larger groups) that all have the same stopping time. We just need to find two numbers $k_1$ and $k_2$ whose iterates join up after the same number of even and odd iterations. Then, if we let $a$ be one more than the number of even iterations, $k_1 + 2^am$ and $k_2 + 2^am$ will join up, and have the same number of stopping times.
When using the above, note that we don't have to stop when our $k_1$ or $k_2$ gets to $1$. Even if the Collatz iterates join up after one has begun the $1, 2, 4$ cycle, adding $2^am$ (for $m > 0$) to each will still mean that the Collatz iterates will join, but this time before the iterates get to $1$. You might notice this phenomenon, for example, with $4 + 2^5m, 5 + 2^5m, 6 + 2^5m$, where we get:
\begin{array}{c}
4 + 2^5m & 2 + 2^4m & \color{red}{1 + 2^3m} & \color{blue}{4 + 2^33m} & 2 + 2^23m & 1 + 2^13m & 4 + 2^13^2m \\
5 + 2^5m & 16 + 2^53m & 8 + 2^43m & \color{blue}{4 + 2^33m} & 2 + 2^23m & \color{red}{1 + 2^13m} & \color{blue}{4 + 2^13^2m} \\
6 + 2^5m & 3 + 2^4m & 10 + 2^43m & 5 + 2^33m & 16 + 2^33^2m & 8 + 2^23^2m & \color{blue}{4 + 2^13^2m}
\end{array}
You can see where the Collatz iterates merge, highlighted in blue. For $m > 0$, this proves that all three numbers have the same stopping time. For $m = 0$, i.e. for $4, 5, 6$, the cycles reach $1$ (highlighted in red) too soon for the stopping times to be equal. This is why $4, 5, 6$ have different stopping times, but $4 + 2^5m, 5 + 2^5m, 6 + 2^5m$ all have the same stopping time for $m > 0$ (explaining that recurring patch of $3$ consecutive numbers with the same stopping time, starting below the first line).
Essentially, once you get a pair of consecutive numbers whose Collatz iterates join after the same number of even and odd steps, you will get infinitely many more pairs with the same property, all of which are pairs of consecutive numbers with the same stopping time.
Explaining the "chunks"
Pairs of numbers with the same stopping time will also propagate further through doubling. If we know that $k_1 + 2^am$ and $k_2 + 2^am$ have the same stopping time, then so will $2k_1 + 2^{a+1}m$ and $2k_2 + 2^{a+1}m$. Or if $a$ is sufficiently large (i.e. we have even steps to spare), then $2k_1 + 2^am$ and $2k_2 + 2^am$ will still do the trick.
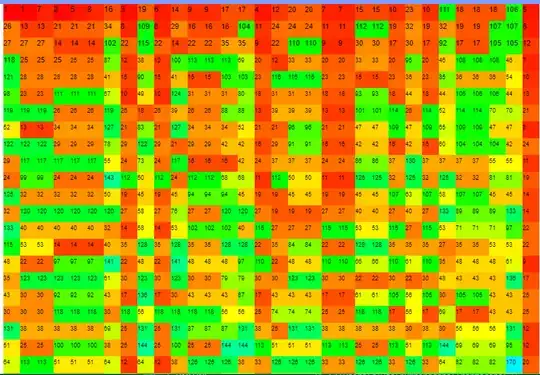
Thus, pairs of consecutive numbers with the same stopping time beget pairs of consecutive even numbers with the same stopping time, and similarly for pairs of numbers divisible by $4$, etc. This way, we get columns of numbers with the same stopping time, which are often a power of $2$ apart.
That said, there are exceptions. For example, the columns for $16 + 2^5$ and $21 + 2^5$ seem to have the same stopping time. But even this is a result of propagation with powers of $2$, though indirectly.
We see that $16 + 2^5m$ and $20 + 2^5m$ both seem to have the same stopping times. Two even steps later, we get $4 + 2^3m$ and $5 + 2^3m$, and as we saw from the example I worked out, only two even steps (and one odd step) are necessary before $4$ and $5$ join each other. So, it makes sense that $16 + 2^5m$ and $20 + 2^5m$ have the same stopping time; it just reduced to a consecutive pair.
Similarly, $20 + 2^5m$ and $21 + 2^5m$ have the same stopping time, and this can (once again) be traced back to $4 + 2^3m$ and $5 + 2^3m$. we can write $20 + 2^5m = 4 + 2^3(4m + 4)$ and $21 + 2^5m = 5 + 2^3(4m + 4)$, and so, once again, we get the same stopping time. Thus, $16 + 2^5m, 20 + 2^5m$, and $21 + 2^5m$ will have the same stopping times, for $m \ge 1$ at least!
On this point, when you plot with $2^5$ columns, patterns that repeat every $2^3$ (or any power of $2$ lesser than $2^5$ will repeat multiple times. From this $4 + 2^3m$ and $5 + 2^3m$ case, we get not only $4 + 2^5m$ and $5 + 2^3m$, but also $12 + 2^5m$ and $13 + 2^5m$, as well as $20, 21$ and $28, 29$. So, what looks like four pairs of columns is really just one pair of columns split into four.
Another way to propagate is to reverse an odd step. You won't see these patterns so clearly in your grid, since reversing an odd step requires $m$ to be divisible by $3$ (as well as other constraints), so you would not see this every row.
Conclusion
I think what we are seeing are a small number of special cases where the Collatz iterates join up early, after the same number of even and odd iterations. These special cases then propagate themselves into larger, more complicated-seeming patterns. In this way, special cases borne out of small numbers running into each other grow and appear much more significant than they really are.