Conditional covariance of two independent normal variables when their sum is fixed

Question

I am reading through Brady Neal's "Introduction to Causality" course textbook and have got to Section 3.6 where Berkson's paradox is discussed. Neal provides the following toy example:

$$ X_{1} = \mathcal{N}(0,1) \\ X_{3} = \mathcal{N}(0,1) \\ X_{2} = X_{1} + X_{3} $$

He then proceeds to compute the covariance of $X_{1}$ and $X_{3}$ as a sanity check:

$$ \text{Cov}(X_{1}, X_{3}) = \mathbb{E}[X_{1}X_{3}] - \mathbb{E}[X_{1}]\mathbb{E}[X_{3}] = \mathbb{E}[X_{1}X_{3}] = \mathbb{E}[X_{1}]\mathbb{E}[X_{3}] = 0 $$

where we used independence. Next Neal computes the conditional covariance given that $X_{2} = x$.

$$ \text{Cov}(X_{1}, X_{3} \,|\, X_{2} = x) = \mathbb{E}[X_{1}X_{3} \,|\, X_{2} = x] = \mathbb{E}[X_{1}(x - X_{1})] = x\mathbb{E}[X_{1}] - \mathbb{E}[X^{2}_{1}] = -1 $$

Is this correct?

When I do my own calculation I seem to get the following result:

$$ \text{Cov}(X_{1}, X_{3} \,|\, X_{2} = x) = \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] - \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{3}\,|\,X_{2}=x] $$

Consider each factor separately in the second term:

$$ \mathbb{E}[X_{1} \,|\, X_{2} = x] = \mathbb{E}[X_{1} \,|\, X_{1} + X_{3} = x] = \mathbb{E}[x - X_{3}] = x - \mathbb{E}[X_{3}] $$

Likewise we have

$$ \mathbb{E}[X_{3} \,|\, X_{2} = x] = x - \mathbb{E}[X_{1}] $$

Multiplying both terms we have:

$$ \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{3}\,|\,X_{2}=x] = (x - \mathbb{E}[X_{3}])(x - \mathbb{E}[X_{1}]) = x^{2} $$

Now consider the first term:

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \mathbb{E}[X_{1}X_{3}\,|\, X_{1} + X_{3} = x] = \\ \mathbb{E}[X_{1}(x - X_{1})] = x\mathbb{E}[X_{1}] - \mathbb{E}[X_{1}^{2}] = 0 - 1 = -1 $$

Putting everything together we have:

$$ \text{Cov}(X_{1}, X_{3} \,|\, X_{2} = x) = \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] - \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{3}\,|\,X_{2}=x] = -1 - x^{2} $$

Am I doing something wrong? I am concerned the author is forgetting that the expectations in the second term are conditional leading them to set the second term to zero as in the unconditioned case. I may also be using the wrong definition for conditional covariance, although no explicit definition is provided in the book.

Note that this example is an attempt to model a collider where $X_{1}$ and $X_{3}$ are parents of $X_{2}$.

EDIT: Both myself and the textbook are wrong!

Thanks to Henry for pointing this out, whose answer I have accepted below. I thought I would correct my approach using Henry's working to highlight my errors.

As before we have:

$$ \text{Cov}(X_{1}, X_{3} \,|\, X_{2} = x) = \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] - \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{3}\,|\,X_{2}=x] $$

Let's deal with the second term first. Clearly we have:

$$ \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{1}\,|\,X_{2}=x] = \mathbb{E}[X_{1}\,|\,X_{2}=x]^{2} $$

Applying the first formula derived by Henry in this question we have

$$ \mathbb{E}[X_{1}\,|\,X_{2}=x]^{2} = \frac{x^{2}}{4} $$

Now for the first term we have

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \mathbb{E}[(x-X_{3})X_{3}\,|\, X_{2} = x] = x\mathbb{E}[X_{3}\,|\, X_{2} = x] - \mathbb{E}[X_{3}^{2}\,|\, X_{2} = x] $$

Note how the conditional in the expectation remains as $X_{3}$ is still conditioned on $X_{2}$. This is what caused the issue with my analysis! Following a similar logic as above with $X_{3}$ in place of $X_{1}$ we have:

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \frac{x^{2}}{2} - \mathbb{E}[X_{3}^{2}\,|\, X_{2} = x] $$

Adding and subtracting $\mathbb{E}[X_{3}\,|\,X_{2} = x]^{2}$ we have

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \frac{x^{2}}{2} - (\mathbb{E}[X_{3}^{2}\,|\, X_{2} = x] - \mathbb{E}[X_{3}\,|\,X_{2} = x]^{2}) - \mathbb{E}[X_{3}\,|\,X_{2} = x]^{2} $$

Observe that the term in the brackets is simply the conditional variance of $X_{3}$. Hence, using the second identity provided by Henry in the aforementioned question we have:

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \frac{x^{2}}{2} - \frac{1}{2} - \mathbb{E}[X_{3}\,|\,X_{2} = x]^{2} $$

Recall that we calculated the leftover term (with $X_{1}$ in place of $X_{3}$. Plugging in our solution we have:

$$ \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] = \frac{x^{2}}{2} - \frac{1}{2} - \frac{x^{2}}{4} = \frac{x^{2}}{2} - 1/2 $$

Putting everything together we end up with:

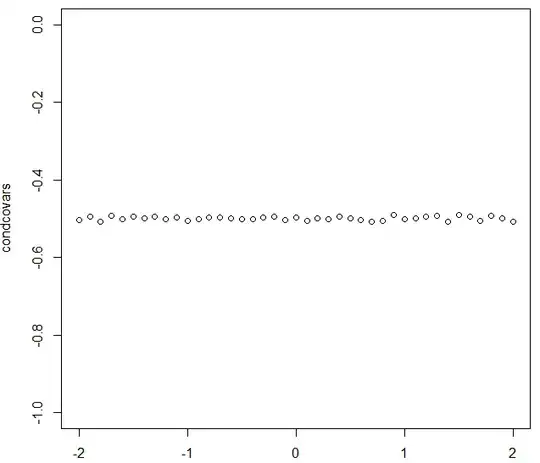
$$ \text{Cov}(X_{1}, X_{3} \,|\, X_{2} = x) = \mathbb{E}[X_{1}X_{3}\,|\, X_{2} = x] - \mathbb{E}[X_{1} \,|\,X_{2}=x]\mathbb{E}[X_{3}\,|\,X_{2}=x] \\ = \frac{x^{2}}{2} - 1/2 - \frac{x^{2}}{4} = -1/2 $$

Finally, we arrive at the correct result! Note that I have left some details out regarding how the conditional expectations and variances used from Henry's question are calculated. Although, I believe a question which presents the working for a similar problem is linked there. I may add these derivations later but for now I am happy to assume that Henry is a divine oracle capable of correctly computing the conditional moments of normal distributions :).

Answer 1

Conditioned on $X_1+X_3=x$, $X_1$ has a conditional distribution which is $N(\frac x2, \frac12)$. So too does $X_3$. This stats.stackexchange gives a more general version

So each of their conditional variances is $\frac12$ and their conditional covariance is then $-\frac12$. This does not vary with $x$.

Here is a simulation in R illustrating this, conditioning on cases close to $x$ values from $-2$ to $2$

set.seed(2022)
cases <- 10^6
X1 <- rnorm(cases)
X3 <- rnorm(cases)
X2 <- X1 + X3
condcovars <- numeric(41)
for (i in (-20):20){
 close <- X2 > i/10 - 1/20 & X2 < i/10 + 1/20
 condcovars[i+21] <- cov(X1[close], X3[close])
 }
names(condcovars) <-  (-20:20)/10
condcovars
-2       -1.9       -1.8       -1.7       -1.6       -1.5       -1.4
-0.5042118 -0.4943630 -0.5069618 -0.4920338 -0.5013615 -0.4952248 -0.4984781
-1.3       -1.2       -1.1         -1       -0.9       -0.8       -0.7
-0.4946318 -0.5015043 -0.4978977 -0.5051132 -0.5016172 -0.4964760 -0.4979527
-0.6       -0.5       -0.4       -0.3       -0.2       -0.1          0
-0.4991278 -0.5020100 -0.5010565 -0.4961058 -0.4952697 -0.5034277 -0.4959253
0.1        0.2        0.3        0.4        0.5        0.6        0.7
-0.5054419 -0.4998629 -0.5007847 -0.4957954 -0.4983496 -0.5031784 -0.5067993
0.8        0.9          1        1.1        1.2        1.3        1.4
-0.5063600 -0.4913827 -0.5006796 -0.4986025 -0.4936689 -0.4922959 -0.5081856
1.5        1.6        1.7        1.8        1.9          2
-0.4911572 -0.4945096 -0.5052851 -0.4933594 -0.4996732 -0.5070671
plot((-20:20)/10, condcovars , ylim=c(-1,0))