Proof of Maximum Principle for Harmonic Functions

Question

A harmonic function is one which solves Laplace's Equation $\Delta u=0$. The maximum principle states that over some domain $D$, $u$ achieves a maximum and minimum on $\partial D$, and nowhere inside $D$.

I am struggling to understand the proof of this principle. I am new to proofs and I would appreciate an appeal to physical intuition much more than a rigorous mathematical proof. Here are my questions:

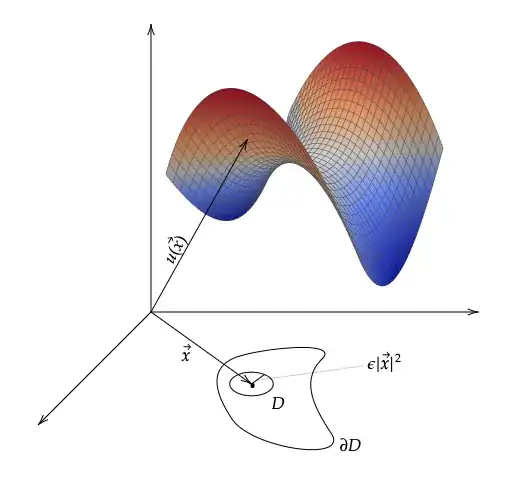
1. One proof is to consider a point $v(\vec{x})=u(\vec{x})+\epsilon | \vec{x}|^2$ where $\vec{x}=(x,y)$ and $|x|=(x^2+y^2+z^2)^{\frac{1}{2}}$. Then, $\Delta v= \Delta u + \epsilon \Delta (x^2+y^2)=0+4\epsilon >0$. But a maximum has $\Delta v\leq0$, thus a contradiction. Would this be akin to the geometric interpretation shown below? If not, what would $u(\vec{x}), v(\vec{x})$, and $\epsilon|x|^2$ actually look like? In addition, $\epsilon|x|^2$ seems like a scalar, and yet we are adding it to the vector $u(\vec{x})$.
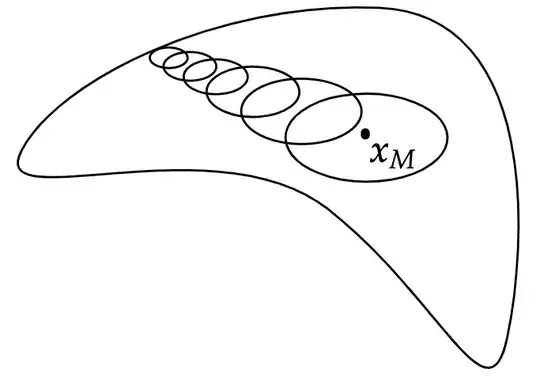
2. Another proof assumes a maximum $x_M\in D$. Then all the points equidistant from $x_M$ must have an average value of $x_M$, by the mean value theorem. But if $x_M$ is the maximum, all these points $x\leq x_M$. Thus, $x=x_M$ for all $x$ on that circle. We repeat this argument, drawing more circles until we reach the boundary. But how does this prove the maximum principle? It seems to work only for circles, for one, and not an arbitrarily shaped domain. In addition, I don't quite understand how the mean value theorem implies that the average value of $x$ on the circle must be $x_M$.

Any help is much appreciated. Again, I would greatly appreciate an appeal to physical intuition as opposed to rigorous mathematics.

Answer 1

1. Your figure is strange. First you are mixing vector $x$ and coordinate $x$, which is not a big deal but still can cause confusion. Second, $u(x)$ (I will use $x$ as a vector) is a scalar, of course, since $u\colon D\longrightarrow \mathbb R$, so no contradiction arises. In this proof you need to construct a smart $v$ out of $u$, such that $\Delta v>0$. In this case the (weak) maximum principle is true for $v$ and, by taking limit $\varepsilon\to 0$, is true for $u$. So here you prove that maximum (and minimum) of $u$ is on the boundary.

If my explanation is still too short for you, check this link, it is probably the cleanest presentation on various forms of maximum principle for elliptic and parabolic problems.

2. Here you prove strong maximum principle, i.e., if maximum of $u$ is inside $D$ then $u$ is a constant on $\overline{D}$. Note that this statement implies the first one. Indeed, to make sure the given proof is working, you need to assume something else about $D$, in particular, you can assume that $\partial D$ is smooth. See the link above about discussion of admissible $D$.

Finally, to show that mean value property implies what you need, let me fix the notation.

Let $p\in D$ be such that $u(p)=m$ and I will assume that $m$ is a minimum of $u$ (the same argument will work for maximum). Let $B_p(R)$ be the ball of radius $R$ with center $p$ and let $|B_R(p)|$ be its measure. Mean value property means that $$ m=u(p)=\frac{1}{|B_R(p)|}\int_{B_R(p)}u $$

Now, take any $q\in B_R(p)$ and consider the ball $B_\epsilon(q)\in B_R(p)$. $B_\epsilon^c(q)$ will denote the complement of $B_\epsilon(q)$ in $B_R(p)$.

Let me assume that $q$ and $\epsilon$ are chosen such that $u(q)>u(p)=m$ and $u(y)\leq m$ for all $y\in B_\epsilon(q)$ and look for contradiction.

I have $$ m=u(p)=\frac{1}{|B_R(p)|}\int_{B_R(p)}u=\frac{1}{|B_R(p)|}\left(\int_{B_\epsilon(q)}u+\int_{B_\epsilon^c(q)}u\right)=\\ \frac{1}{|B_R(p)|}\left(\frac{|B_\epsilon(q)|}{|B_\epsilon(q)|}\int_{B_\epsilon(q)}u+\int_{B_\epsilon^c(q)}u\right)\geq\\ \frac{1}{|B_R(p)|}\left(|B_\epsilon(q)|u(q)+m|B^c_\epsilon(q)|\right)>\\ \frac{m}{|B_R(p)|}\left(|B_\epsilon(q)|m+m|B^c_\epsilon(q)|\right)>\\ m, $$ and the required contradiction is reached.

Answer 2

Your proof 1 shows that if $\Delta u \geq 0$ then $u$ attains its maximum on the boundary of $D$. The only purpose of the $\varepsilon |x|^2$ is to elevate the hypothesis to $\Delta u > 0$ so that the proof works.

Integrate the mean value property for circles to see that the mean value property is true for balls too. Suppose $u$ is harmonic and attains a maximum at some $x_0 \in D$. Then using the mean value theorem for balls it is not hard to show that $u(x) = u(x_0)$ for all $x$ in some ball containing $x_0$. Now consider $S = \{x \in D : u(x) = u(x_0)\}$. The above argument shows that $S$ is open. $S$ is closed by continuity of $u$. So if $D$ is connected, then $S = D$. This is the strong maximum principle. The assumption of the connectedness of $D$ is what allows the "spreading" argument to be made rigorous.