Variational Calculus - Derivation of Lagrangian Equation

Question

While learning about the calculus of variations to look at the principle of least action, we arrive at a point where we want to minimise the following functional (or of similar form):

$$S(y(x),y'(x),x) = \int_{x_{1}}^{x_{2}} \sqrt{1+\left(\frac{dy}{dx}\right)^2} \, dx$$

We start of by creating a 'corrected' function of the following form:

$\Upsilon = y(x) + \eta(x)$ such that $\eta(x_{1}) = \eta(x_{2}) = 0.$

Whilst doing so, we say that $\eta(x)$ is continuous and differentiable.

I don't understand why $\eta(x)$ needs to be differentiable. Isn't it just a function that allows us to look at all the possible paths from $x_{1}$ to $x_{2}$? Why do these paths need to be differentiable? Why can't these paths have corners?

Answer 1

It needs to be differentiable since when you take the difference quotient of $S$ you'll notice that the derivative of $\eta$ appears as follows:

$$S[y+\epsilon\eta]=\int \sqrt{1+\bigg(\dfrac{d(y+\epsilon \eta)}{dx}\bigg)^2}=\int \sqrt{1+\bigg(y'(x)+\epsilon\eta'(x)\bigg)^2}$$

If $\eta$ is non differentiable then this difference quotient is meaningless. But you need it to take the derivative.

$$\lim_{\epsilon \to 0}\dfrac{1}{\epsilon}(S[y+\epsilon \eta]-S[y])$$

And eventually obtain Euler-Lagrange.

Answer 2

It has to be Continuous because we want only Continuous Solutions.

It has to be Differentiable because we use the Derivative while "Deriving" or "Deducing" the Euler–Lagrange equation.

The Euler–Lagrange equation is true only when considering such η(x) & It may not be true for other η(x) which are either not continuous or not Differentiable.

Have a look here :
(1) https://en.wikipedia.org/wiki/Calculus_of_variations#Euler%E2%80%93Lagrange_equation

"[....] η(x) is an arbitrary function that has at least one derivative and vanishes at the endpoints [....]"

"Taking the total derivative [....] , where y=f+εη and y′=f′+εη′ are considered as functions of ε rather than x [....]"

(2) https://en.wikipedia.org/wiki/Euler%E2%80%93Lagrange_equation

Here too we have the same "Derivation".

Answer 3

About the reason for imposing the condition that the added variation $\eta(x)$ should be continuous and differentiable:

The way that Jacob Bernoulli solved the Brachistochrone problem also underlines that reason.

The challenge of solving the Brachistochrone problem had been issued by Johann Bernoulli, the younger brother of Jacob Bernoulli.

As we know, it was in the wake of the Brachistochrone challenge calculus of variations was developed, which means that when Jacob Bernoulli took up the challenge he did not have calculus of variations, nor any precursor of it.

Jacob Bernoulli recognized a particular feature of the brachistochrone problem, and he presented that feature in the form of a lemma:

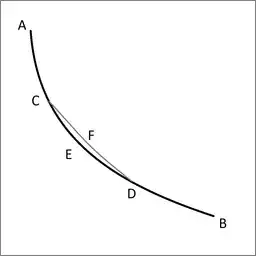
Let ACEDB be the desired curve along which a heavy point falls from A to B in the shortest time, and let C and D be two points on it as close together as we like. Then the segment of arc CED is among all segments of arc with C and D as end points the segment that a heavy point falling from A traverses in the shortest time. Indeed, if another segment of arc CFD were traversed in a shorter time, then the point would move along AGFDB in a shorter time than along ACEDB, which is contrary to our supposition.

(Acta Eruditorum, May 1697, pp. 211-217)

Let me rephrase what Jacob Bernoulli had recognized:
Take the solution to the Brachistochrone problem, and take a arbitrary subsection of that curve. That subsection is also an instance of solving the brachistochrone problem. This is valid at any scale; down to arbitrarily small scale.

This informed Jacob Bernoulli: a differential equation exists that solves the Brachistochrone problem. Of course, it did not provide a tangible clue what that differential equation is. I like to think that knowing that it must exist gave Jacob Bernoulli the perseverence to carry the problem to the end.

The condition of the derivative of the integral being zero is a remarkably constraining condition.

Jacob's lemma, generalized:
In order for the derivative of $\int_{x_1}^{x_2}$ to be zero: for every subsection anywhere between $x_1$ and $x_2$ the derivative of the corresponding integral must be zero.

As we know: the Euler-Lagrange equation transforms any problem that is stated in variational form to a differential equation.

The fact that every variational form can be transformed to differential form shows that the variational form was a differential form all along.

The fact that the variational form is a differential form can be seen as follows: you are looking for a curve such that at every subsection along the curve the derivative of the integral is zero. It is taking the derivative that counts.

(The derivation of the Euler-Lagrange equation is a process of stripping down to what is sufficient. Some elements do not make it to the Euler-Lagrange equation; those are superfluous. Taking the derivative makes it to the Euler-Lagrange equation; the integration on the other hand does not make it to the Euler-Lagrange equation.)

So: it is necessary that $\eta(x)$ is differentiable.