Solve for $x$ in $x^y - x = 1$.

Asked Jul 27 '22 at 18:54

Active Jul 27 '22 at 18:54

Viewed 89 times

Consider the equation $x^y - x = 1.$ I'd like to find a closed form expression for $x$ in terms of $y$. It's pretty easy to solve for $y$ in terms of $x$:

$y = \dfrac{\ln(x+1)}{\ln(x)}\tag*{}$

Obviously there are domain restrictions here: $x>0, x\ne 1$. However, I have no idea how to find the inverse function. A quick graph of the equation suggests that $x$ is indeed a function of $y,$ defined for all $y \notin (0, 1]$:

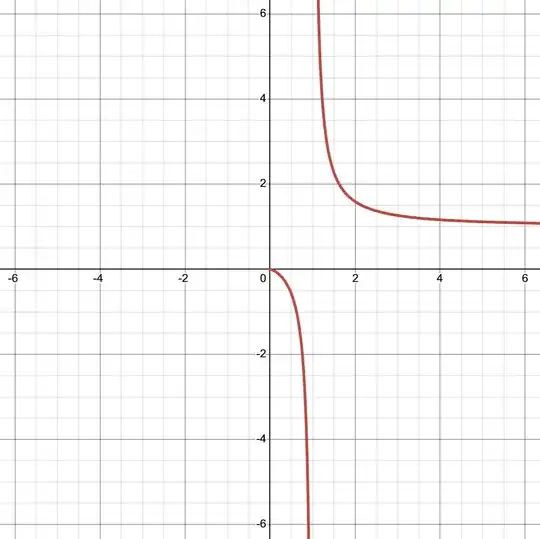Plot of <span class= $x^y - x = 1$" />

asked Jul 27 '22 at 18:54

Ted Hopp

@Doug: How do you get that? – Dan Jul 27 '22 at 19:06
@Dan, My bad ... I was just being dumb – Jul 27 '22 at 19:10
Having an inverse does not imply having a close form of an inverse. – Fede Poncio Jul 27 '22 at 19:23
FWIW, I tried Wolfram Alpha, but just got "Standard computation time exceeded..." – Dan Jul 27 '22 at 19:24
2

Looks like duplicate of How to solve $x^y=ax−b$ with $a=1$ and $b=-1$. – emacs drives me nuts Jul 27 '22 at 19:49
1

Does this answer your question? How to solve $x^y = ax-b$ – Dan Jul 27 '22 at 19:50
This question has an answer at https://math.stackexchange.com/questions/257455/inverse-function-of-y-frac-lnx1-ln-x/4494271#4494271. – IV_ Jul 27 '22 at 20:45

Solve for $x$ in $x^y - x = 1$.

0 Answers0