For a general max flow problem, we know that each intermediatte node must give away the same amount of flow it receives. Besides this, we also know that the amount of flow that leaves the origin node ($s$) should be the same amount received by the last node ($t$).
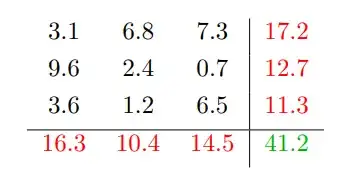
Now, take the following matrix as an example:
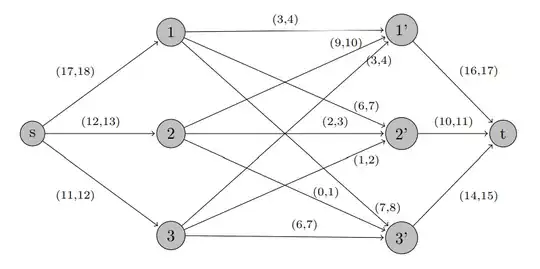
The transformation into a max flow problem comes with the following graph:
And my question now is pretty simple... Take for example the node $1$. It receives $17$ amount of flow and only gives away $3+6+7 = 16 \neq 17$. On the other hand, take the node $1'$ for example. It receives $3+3+9 = 15$ and it gives away $16$. I believe this doesn't agree with the basic properties I introduced earlier.
Is there any explanation for this?