Trying to model the Flyby anomaly

Question

Thinking about it, the following non-linear ordinary differential equation crossed my mind: $$ \frac{d^2 r}{dt^2} - \frac{1}{2} H \frac{dr}{dt} + \frac{\mu}{r^2} = 0 $$ Apparently, I've been trying to modify and simplify an equation for Orbital motion.
The physical meaning of the variables is: $r=$ position , $t=$ time , $(H,\mu)=$ constants.
The constant $H$ may be considered as being very small. An obvious simplification is $H=0$: $$ \frac{d^2 r}{dt^2} = - \frac{\mu}{r^2} $$ An equation which can be solved as follows. Physicists will recognize kinetic and potential energy. $$ \frac{d^2 r}{dt^2}\frac{dr}{dt} = - \frac{\mu}{r^2}\frac{dr}{dt} \\ \frac{1}{2} \frac{d}{dt}\left(\frac{dr}{dt}\right)^2 = \frac{d}{dt}\left(\frac{\mu}{r}\right) \\ v^2 = \left(\frac{dr}{dt}\right)^2 = \frac{2\mu}{r} + C $$ With $C$ as an integration constant. It can be determined by assuming that speed $v=V$ at infinity $r\to\infty$ is given: $$ \left(\frac{dr}{dt}\right)^2 = \frac{2\mu}{r} + V^2 = \mu \left( \frac{2}{r} - \frac{1}{a} \right) $$ The result is written in the latter form because it resembles (not at all by coincidence) the Vis-viva equation, with $a = -\mu/V^2 \lt 0$ for a hyperbola.
Calculations can be continued eventually for finding the position as a function of time. Which is not quite easy, and not interesting too, for our purpose.
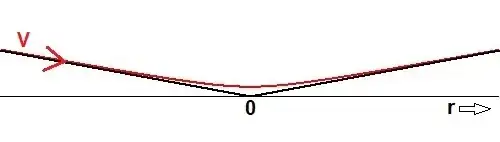
I think that the one-dimensional model may be acceptable as the simplification of a rather straight hyperbolic trajectory:

Because in that case the asymptotes of the hyperbola could replace the hyperbola itself as a first approximation (except for the singularity near $r=0$).
But let us return to the core of the question, which is my tentative non-linear ODE for the Flyby anomaly. Problem is that I have not a clue how to solve it. $$ \frac{d^2 r}{dt^2} - \frac{1}{2} H \frac{dr}{dt} + \frac{\mu}{r^2} = 0 $$ Or equivalently: $$ \left(\frac{d}{dt} - H \right) \left(\frac{dr}{dt}\right)^2 = \frac{d}{dt}\left(\frac{2\mu}{r}\right) $$ Which doesn't help me any further.
Any ideas? I'm satisfied with a solution for $\,v=dr/dt\,$ only, even if it's approximate.

Answer 1

Taking $r'(t)=v(r)$, and thus $r''=vv'_r$, we get that \begin{align} vv'_r-\frac{H}{2}v+\frac{\mu}{r^2}=0. \end{align} Now taking $r=2\xi/H$ we bring it to an Abel equation of the second kind in the usual form \begin{align} vv'_{\xi}-v=-\frac{\mu H}{2}\xi^{-2}. \end{align} The parametric solution to this problem is given in the 'Handbook of Exact Solutions for Scientists and Engineers 2ed.' as (I'm copying from text here)

"

\begin{align}\tag{1} \xi=2a\tau^{4/3}Z^2U_2^{-1},\quad v=\pm3a\tau^{-2/3}Z^{-1}U_2^{-1}U_3, \quad \text{where} \quad a^3=\frac{\mu H}{72}, \end{align} where the following notations are used \begin{align} Z_{\nu}&=\begin{cases} C_1J_{\nu}(\tau)+C_2Y_{\nu}(\tau), \ \ \text{for the upper sign},\\ C_1I_{\nu}(\tau)+C_2K_{\nu}(\tau), \ \ \text{for the lower sign}, \end{cases}\\ f_{\nu}=\tau (Z_{\nu})'_{\tau}+\nu Z_{\nu}, \ \ Z&=Z_{1/3}, \ \ U_1=\tau Z'_{\tau}+\frac{1}{3}Z,\ \ U_2=U_1^2\pm\tau^2Z^2, \ \ U_3=\pm\frac{2}{3}\tau^2Z^3-2U_1U_2, \end{align} $J_{\nu}(\tau)$ and $Y_{\nu}(\tau)$ are the Bessel functions, and $I_{\nu}(\tau)$ and $K_{\nu}(\tau)$ are the modified Bessel functions.

Remark. The solutions of these equations contain only the ratio $Z'_{\tau}/Z$ [...] Therefore, for symmetry, function $Z$ is defined in terms of two "arbitrary" constants $C_1$ and $C_2$ (instead, we can set, for instance, $C_1=1$ and $C_2=C$)."

Here's where I'm not too sure. For brevity, denote the solutions in equation (1) as \begin{align} r=F(\tau),\quad r'=G(\tau). \end{align} Where I've used the equalities $r=2\xi/H$ and $v=r'$. Taking a derivative we arrive at \begin{align} \frac{\mathrm d\tau}{\mathrm dt}F'(\tau)=G(\tau)\longrightarrow t=C_3+\int\frac{F'(\tau)}{G(\tau)}\mathrm d\tau. \end{align} Then the parametric solution can be written as \begin{align} r=F(\tau),\quad t=C_3+\int\frac{F'(\tau)}{G(\tau)}\mathrm d\tau. \end{align} Quite the convoluted solution, though I'm not entirely sure it's correct. If anyone has observations or has spotted an error please let me know.