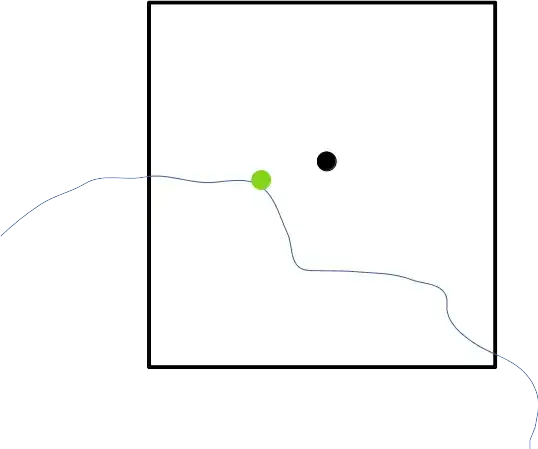
The problem is as follows, you have an implicit function $f:\mathbb{R}^2 \rightarrow \mathbb{R}$.
You have a square region that overlaps with the boundary of the surface described by the iso line $f(x, y) = 0$.
You want a point that is on the surface and that is as far as possible from the boundaries which is equivalent to saying you want it to be as close as possible to the cell center.
The blue curve is the iso surface, the black point the center of the square, the green point a good candidate point.
I am numerically solving the optimum using gradient descent. I devised the following function to minimize:
$$L(X) = \lambda f(X)^2 + \|X - c\|^2$$
I.e. the quality of the solution is the signed distance function squared (whose minimum set is the iso surface $f = 0$ by construction) plus the squared distance between the input point and the cell center $c$.
This, I think is equivalent to saying:
$$\text{ minimize }_{X\in \mathbb{R}^2} \|X - c\|^2$$ $$\text{ subject to } f(X) = 0$$
The algorithm I am using to solve the optimization problem is very simple. Let $g$ be the numeric gradient of $L$ and let $X_0=c$ be the starting point.
For 100 iterations $$X_i+1 = X_i - \epsilon g(X_i)$$
This formulation seems ok, but the solutions I am obtaining are a little off target. By this I mean I encounter many solutions that are around the optimum but far enough that it is noticeable my method did not converge in 100 iterations. I cannot increase the iteration count, so I need to tweak the model.
Any suggestions?