I am slightly confused as to how you calculate Mahalanobis distance given a set of data. I have tried asking my tutor for help but he does not seem interested in helping what so ever and I am continuously insulted. I thought I would turn to the community for help.
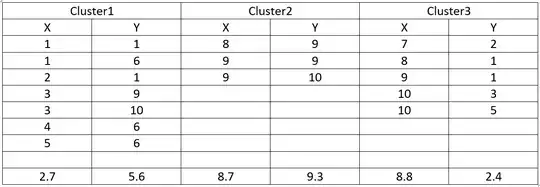
I have a set of data here and I have performed distance calculation once using Euclidean distance to group the data. Now I am looking to calculate distance using Mahalanobis distance. I have calculated the means and also calculated a Pooled covariance matrix. I am unsure as to what I need to do from here to begin calculating distances for each point.
Data clustered into 3 clusters after performing Euclidean distance to place points into initial groups
Pooled Covariance matrix \begin{bmatrix}1.394&1.702\\1.702&6.62\end{bmatrix}
Inverse Pooled Covariance \begin{bmatrix}1.046&-0.269\\-0.269&0.221\end{bmatrix}