Given the red and blue circle, construct with straightedge and compass the yellow one

Question

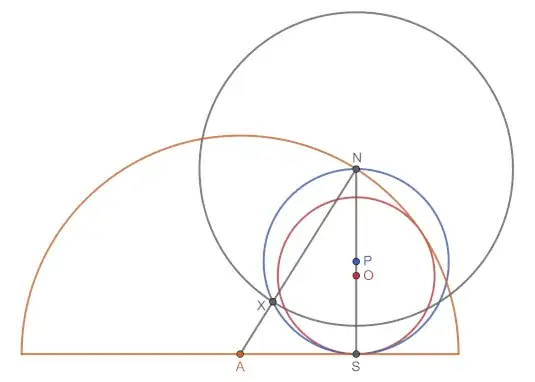
The problem is from the image: the yellow and the red and tangents, so are the blue and the red and the yellow passes through that black thick dot at the north pole of the blue one.

So my attempt:

I had no idea on what to do, maybe some homotheties could help, but not directly... so I did the analytic calculation. Put the $x$ axis on the common tangent line and the origin at the tangency point between red and blue ones.

Call $a$ the radius of the red circle, $b$ the radius of the blue one. $b>a$

So, if $A =(t,0)$, with $t<0$, is the center of the yellow one, then I found:

$t = -\frac{b}{2a} \sqrt{b^2-4a^2}$

which is quite weird because it needs $b>2a$ which clearly is not the case in the figure.

I can't see a mistake in the calculations, the line joining $A$ and the center of the red circle $(0,a)$ is:

$\frac ya + \frac xt = 1$

it is not that hard to find the contact point of the yellow and red one...

tldr: my calculations look weird and I got no synthetic idea of how to solve this one.

Answer 1

Let $NS$ be the diameter of the blue circle through the common tangency point $S$. Draw a circle centered at $N$ whose radius is the red circle’s diameter; let it meet the blue circle at $X$. Let $NX$ meet the common tangent at $A$. Then the desired semicircle has center $A$ and radius $AN$.

Proof: $AO^2 = AS^2 + OS^2 = AN⋅AX + OS^2 = AN(AN - 2OS) + OS^2 = (AN - OS)^2$.

Answer 2

Using radius of the red circle as $a$, of the blue circle as $b$ and of yellow semi-circle as $R$, and $t$ as the distance between center of the yellow semi-circle and the common tangent of the blue and red circle, below are two equations we need to solve -

$R^2 = (2b)^2 + t^2 \tag1$
$(R-a)^2 = a^2 + t^2 \tag1$

Solving, $ ~\displaystyle t = \frac{2b \sqrt{b^2 - a^2}}{a}, ~R = \frac{2b^2}{a}$

Answer 3

In the diagram, the blue circle has center $G$, and diameter $AB$. The red circle has center $E$. The dotted curve is a hyperbola with foci $B,E$ and passes through $G$. $F$ is a general point on the hyperbola. The green circle has center $F$ and passes through $B$. The ray $FE$ intersects the red circle at $H$.

We want to show that $FH=FB$. If so, $H$ is on the the green circle, and the green circle is tangent to the red circle. It follows that if $F$ is either of the intersections of the hyperbola with the tangent at $A$, e.g. $X$, then the green circle will be the circle requested in the question.

A compass and straightedge construction of this intersection is given at the answer to Given the two foci and the vertices of an hyperbola and a random line how can one construct the meetings of the curves?

It remains to show that $FH=FB$. For ease of reading, let $R,r$ be the radii of the blue and red circles respectively. For a point $F$ on a hyperbola, the difference of the distances to the foci is a constant. So $$ FB-FE=k=BG-EG=R-(R-r)=r \\ \implies FE=FB-r \\ \implies FH=FE+EH=FB-r+r=FB \\ \implies FH=FB. $$

I haven't looked closely at the hyperbola/line intersection construction. There may be some shortcuts because the line in question is parallel to the minor axis of the hyperbola.