10

This question is based on a Puzzling Stack question I answered.

Suppose you have a loaded $10$-sided die that gives one value with probability $\frac7{25}$ and the rest with probability $\frac2{25}$ each, but you do not know the favoured value. A maximum likelihood method to determine this favoured value is as follows:

  1. Set probabilities $p_1=\dots=p_{10}=\frac1{10}$, where $p_i$ is the likelihood of $i$ being the favoured value.
  2. Roll the die repeatedly; for each value $c$ that comes up multiply $p_c$ by $3.5$, the ratio of probabilities of a favoured face to an unfavoured face. Normalise after each update and stop when one $p_i$ becomes dominant enough.

This strategy is quite efficient, for simulating it $4121000$ times gave a mean of about $35.47$ rolls until one $p_i$ exceeded $0.99$ and a median of $32$ rolls. The histogram of rolls needed, however, looks very odd with its wavy top:

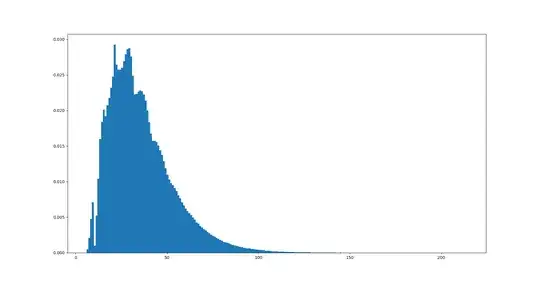
Is there any logical explanation for the histogram's peculiar shape? The number of simulations I made certainly seems high enough to rule out sample size as an explanation.

Here is the histogram corresponding to a d3 with one value twice as likely ($1/2$) to come up as the other two ($1/4$): 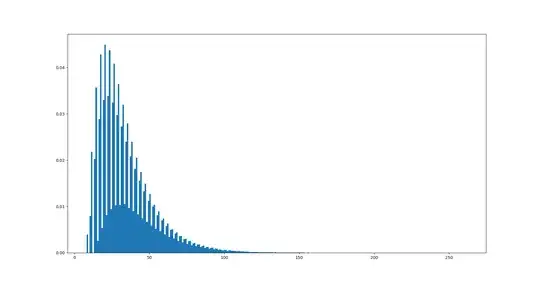Clearly there is a dependence on the number of possibilities, but what kind?

Parcly Taxel
  • 105,904
  • 1
    "The number of simulations I made certainly seems high enough to rule out sample size as an explanation." Not that I disagree, but... If you run it one more time, do you get the waves in the same places? – Arthur Feb 02 '22 at 18:22
  • 1
    @Arthur Yes. The mode seems to be the sharp spike at $21$ rather than some value to the right, given enough trials. – Parcly Taxel Feb 02 '22 at 18:26
  • Suspect the peaks correspond to runs in which the favoured outcome occurred different number of times. – Oscar Cunningham Feb 02 '22 at 19:12
  • 1
    I suspect the convergence is very dependent on the early part of the sequence of tosses, particularly if the same less likely value occurs a few times early on. – copper.hat Feb 02 '22 at 19:48
  • Also, just to be sure, instead of stopping when the $\max$ is over $0.99$, stop when the probs[0] value is over $0.99$, or at least validate that the $\max$ occurs at index zero. – copper.hat Feb 02 '22 at 19:59
  • 2
    @copper.hat I tried stopping at probs[0] $\ge0.99$ – the same wavy shape appears, though the mean increases slightly to about $35.74$. – Parcly Taxel Feb 03 '22 at 01:36
  • My guess is that you are seeing "butterfly" effects due to imprecision in the calculation being magnified. You might try it with a "16 sided die" instead of 10-sided, and see if you get the same weird effect. If you don't, then likely it occurring because $1/10$ is not exactly representable, while $1/16$ is. – Paul Sinclair Feb 03 '22 at 14:04
  • @PaulSinclair How can I be seeing butterflies when the effect shows up even with a $3$-sided die? (It is trivial to show that this effect must appear for a d2, i.e. a biased coin.) – Parcly Taxel Feb 03 '22 at 14:58
  • 1
    I ran your code and collected & printed out the samples whenever it stopped with trials equal to one of 9,10,11. In almost all the 9 cases, there are 6 zeroes and the rest are distinct. In all the 10 cases, there are 7 zeroes and at least one repeat. In most of the 11 cases, there are 7 zeroes and no repeats. I think the first notch just reflects the relative frequencies of these cases. I don't think there is any imprecision involved. – copper.hat Feb 04 '22 at 07:24
  • @ParclyTaxel: I run the equivalent game (the friend choosing randomly a number between 1 and m and being honest with his choice at a .2:.8 ratio) for different $m$'s (2,3,4,5,8,10, 16,20,32, 64) and plotted the stopping time (when the prior is at least .99 for the first time) at its frequency ( instead if histograms to avoid issues with bin size) The smilingly multimodal behavior in the center of the distribution appears between $3\leq m\leq 12$ and start to smooth out the larger the $m$ (also with 4e6 samples). The means and median stopping times also decreasing with $m$. – Mittens Feb 05 '22 at 22:58
  • @OliverDiaz My histogram bin sizes are set to $1$, so they effectively serve as frequency counters. – Parcly Taxel Feb 07 '22 at 04:13
  • @ParclyTaxel: That is what I thought. The point I was trying to make is that the wavy charts seem to be in effect wavy. What is interesting is that as you increase the number of "sides" of your dice, the waviness (with except of outliers that you can only appreciate in log scale) decreases. I created samples for 2 through 15 and then from 16, 32, 64 face dices and the waviness starts to smooth out. – Mittens Feb 07 '22 at 04:29

2 Answers2

6

This can be computed more exactly using a Markov chain, but my impression is that you're looking for some sort of intuitive explanation.

Suppose we rolled all 10 numbers once. Each number would have its factor multiplied by 3.5 (before normalization), but since all numbers get the same factor, the result after normalization is unchanged.

Thus, a crude approximation is that the cumulative process at exit time is the sum of two types of sets of rolls:

  • A set of 1 roll in which only the favored number is rolled, which results in progress towards the 0.99 threshold. Specifically, the favored number's factor has to grow from 1 : 9 to 99 : 1, which is $\log(99 \cdot 9) / \log(3.5) \gtrapprox 5.42$ occurrences of this set.
  • A set of 10 rolls in which each number is rolled once, which results in zero net progress towards the 0.99 threshold.

If this approximation was exact, we would have nonzero probabilities at 6, 16, 26, 36, ... and zero probability everywhere else, since exactly 6 of the first type of set is rolled and some integer number of the second type. This approximation isn't exact, because you will get partial sets of the second type, some non-favored numbers might be rolled more than others, etc. which smooths out those spikes---but not completely.

HighDiceRoller
  • 1,130
6

To corroborate Oscar Cunningham’s comment and HighDiceRoller’s answer, here’s a histogram disaggregated according to the number of times the favoured face came up. The aggregated histogram is the purple one. You can see nicely how it’s composed of the individual components whose spread and overlap increases with the number of favoured rolls; at low values they’re sufficiently separated to make their peaks stand out in the sum.

disaggregated histogram

joriki
  • 242,601