4

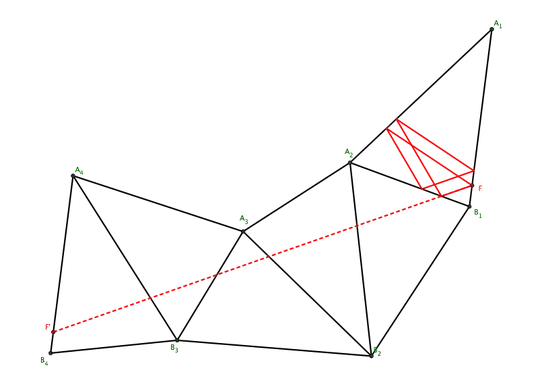
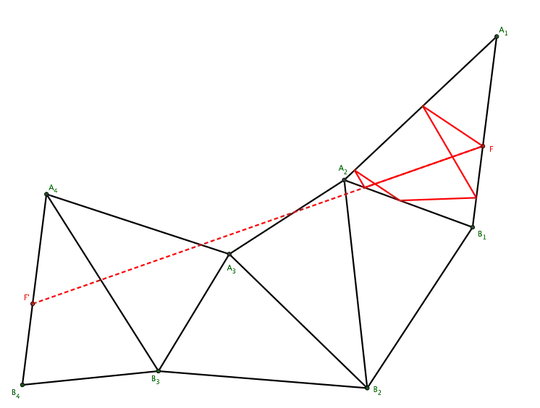
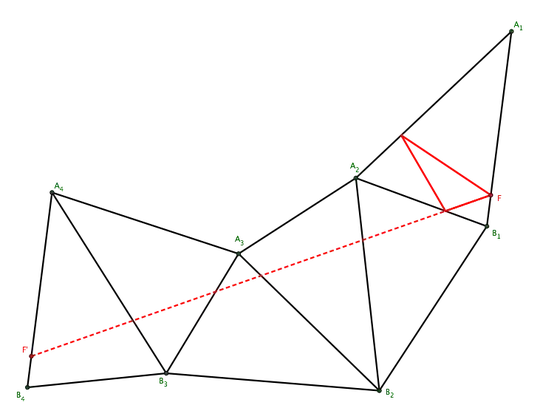
In 2009, Richard Schwartz proved that any obtuse triangle whose largest angle is $\leq100^{\circ}$ has a stable periodic billiard orbit. My question then, is:

How can I reproduce Schwartz's result using a simulation?

More specifically,

How can I develop a numerical method converging to a $(P_0,V_0)$ (initial position, initial direction) giving a Schwartz periodic orbit?

I've created a functioning simulation which produces paths in a triangular billiard table, given the initial position and direction of the ball: 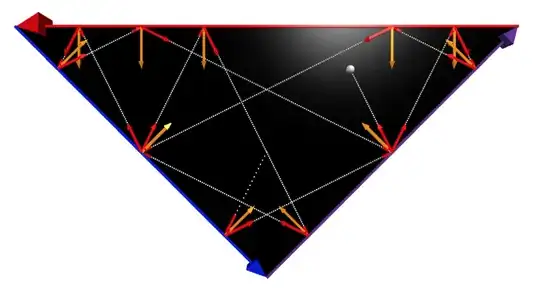enter image description here However, I have no idea how to even begin computationally reproducing Schwartz's result. A brute-force approach of supplying the ball with every initial condition (position, direction) for every triangle with angles $100\leq \alpha \leq 180$ is simply infeasible for an infinite search space. Given this, I would very much appreciate any insights from the Math Stack Exchange community for how to go about reproducing this result. And of course, I can make any modifications to my program as necessary.

Blue
  • 83,939
rb3652
  • 381

1 Answers1

2

The explanation is given in chapter 2 of the cited paper. Every orbit corresponds to an unfolding, which in turn can be described by a "word" formed by digits $123$, a digit for each "bounce" in the orbit, where $1$ represents the shortest side, $2$ the next-shortest side and $3$ the longest side. The first digit in the word represents the starting side. Subsequent digits represent a reflection of the last constructed triangle about one of its sides, giving the next triangle in the unfolding.

If the word satisfies a condition given in Lemma 2.8, then the starting side of the first triangle is parallel to the corresponding side of the last triangle. In this case they show that any straight line joining a starting point $F$ on the starting side with the corresponding point $F'$ on the last side represents a periodic orbit, provided segment $FF'$ lies all within the unfolding.

You can see below an example of closed orbit, taken from the paper (Chapter 2, Figure 1) and corresponding to $W=12323131232313$. Any straight line joining a starting point $F$ on side $A_1B_1$ with the corresponding point $F'$ on side $A_8B_8$, all lying within the unfolding, represents a periodic orbit (dashed line).

enter image description here

EDIT.

One can see below another example, corresponding to $W=213213$. All starting positions $F$ lead to a periodic orbit of period $6$.

enter image description here

Of course one must check that segment $FF'$ be all inside the unfolding, otherwise we get a wrong path (see figure below). Checking is not difficult: line $FF'$ must cross the sides of the triangles in the order given by $W$, as in figure above. If that is not the case (in figure below the order is $213123$) then $FF'$ goes outside the unfolding.

enter image description here

But for a particular position of $F$ the orbit degenerates into twice an orbit of period $3$, see figure below. In that case we could just use the first three triangles, corresponding to $W=213$.

Hence periodic orbits are also possible when the condition of Lemma 2.8 is not satisfied. But they exist only for some positions of starting point $F$.

enter image description here

Intelligenti pauca
  • 55,765
  • Thanks for the idea. I understand the general idea of unfolding and I imagine that I can work backwards from a straight line unfolding to a periodic orbit, but to do so, how can one computationally reproduce such an unfolding? More specifically, perhaps, how does one know how many triangles are needed for an unfolding (is it just the number of digits in a "word"?) and the angle at which to tilt each triangle? – rb3652 Jan 10 '22 at 16:09
  • @rb3652 It's all explained in that paper: you start with a stable word (e.g. $12323131232313$ in the example above) and for each digit you perform a reflection about a side of the triangle: the shortest side if the digit is $1$, the next-shortest edge if the digit is $2$ and the longest edge if the digit is $3$. – Intelligenti pauca Jan 10 '22 at 16:42
  • A word is stable if it verifies Lemma 2.8. And yes: the number of triangles is the same as the length of the word. – Intelligenti pauca Jan 10 '22 at 16:44
  • Say I have a triangle with sides 1,2, and 3, and the program begins by looking for orbits of length 3, starting with 213. It can check if this is a closed orbit in two ways: (1) Simulate a ball hitting side 2 from a discrete set of $(P_0,V_0)$. If any of these paths returns to where it started, success! or (2) The program reflects the triangle three times, first over side 2, then 1, then 3. If there exists a straight line connecting $F$ on side 2 of the first triangle to $F$ on side 2 of the third triangle, a closed orbit has been found. What do you think? – rb3652 Jan 10 '22 at 18:49
  • @rb3652 You must choose the word so that the starting side (first digit: 1 in the above example) is parallel to the last side. Lemma 2.8 explains how to do that: orbit 213 doesn't work, while 213213 does. First and last side are corresponding in a translation, and $F'$ must then be the translated of $F$ (vectors $\vec{A_1A_8}$, $\vec{B_1B_8}$ and $\vec{FF'}$ are equal). – Intelligenti pauca Jan 10 '22 at 19:26
  • I'm not following -- I understand the general idea that the start and end sides must be parallel and indeed I've read Lemma 2.8 (with little insight), but how do you know that 213 will fail but 213213 will not? In addition, what exactly is the advantage of using this second method over the first one (i.e., actually shooting billiards from some $(P_0, V_0)$ to see if they form a closed orbit)? Thank you for your assistance. – rb3652 Jan 10 '22 at 20:02
  • @rb3652 First, we break $W = 213213$ into couplets: $W = 21\ 32\ 13$. Let $N_{ij}$ denote the number of couplets having type $ij$: $N_{12} =0$, $N_{21} =1$, $N_{23} =0$, $N_{32} =1$, $N_{31} =0$, $N_{13} =1$. Lemma 2.8. A word $W$ is stable if and only if $N_{12} −N_{21} = N_{23} −N_{32} = N_{31} −N_{13}.$ In our case all differences are $-1$, hence $W = 213213$ is stable. – Intelligenti pauca Jan 10 '22 at 20:50
  • The difference is you don't have to try an orbit at random, hoping for good luck. You are sure path $FF'$ will give you a closed orbit. – Intelligenti pauca Jan 10 '22 at 20:51
  • Note also that, with your method, it is not enough if the ball returns to its starting point, to have a closed orbit. You must also make sure the direction is the right one. – Intelligenti pauca Jan 10 '22 at 20:57
  • Ah, due to your explanation, I'm beginning to understand. Say, then, the user gives the following input: Search for Closed Orbits of Period Length: 3. The program will then search through all 6 permutations of the numbers 1,2, and 3 (i.e., 123, 213, etc.). It then breaks each permutation (i.e., 213) into 6 couplets, checking if ${12}−{21}={23}−{32}={31}−{13}$. If that condition is indeed satisfied, that means we have a closed orbit! Is this correct? – rb3652 Jan 10 '22 at 21:14
  • Yes, correct. But the method only works for an even period of at least 6. And one must check there is some $FF'$ all inside the unfolding. – Intelligenti pauca Jan 10 '22 at 21:38
  • How exactly would one go about checking if $\exists FF'$ inside the folding? Would I have to actually graphically reflect the triangles and check whether $\exists FF'$? Furthermore, does this mean a closed orbit exists only if ${12}−{21}={23}−{32}={31}−{13}$ and $\exists FF'$? – rb3652 Jan 10 '22 at 22:37
  • @rb3652 See my edit. – Intelligenti pauca Jan 11 '22 at 00:01
  • I've been thinking about this for the last few days. In particular, I've been trying to create an algorithm which performs the first check (checks if word is combinatorially stable). I'm at the last stage of this algorithm, but I have a question. Lemma 2.8 states "A word is stable if and only if $N_{12}-N_{21}=N_{23}-N_{32}=N_{31}-N_{13}$". This is all good and fine. But, I have a question: If we disregard the second condition (i.e., unfolding), what triangles is the first condition valid for? Surely 213213 is not a periodic path in all triangles? Or am I missing something? – rb3652 Jan 16 '22 at 23:37
  • @rb3652 To have a periodic and stable path you must also make sure that $FF'$ be inside the unfolding, and for some triangles that is never possible. – Intelligenti pauca Jan 17 '22 at 15:09
  • Oh, I see. So that's why the second condition matters. – rb3652 Jan 17 '22 at 16:15
  • Just to be absolutely certain, for testing any periodic billiard path $P_i$, we have two filters: combinatorially stable and line within unfolding. If the orbit fails the first filter, it is automatically disqualified from being a periodic path. If it does, however, pass the first filter, the second filter is checked. If it passes, the orbit is declared periodic. Otherwise, it is not. Would this be correct? – rb3652 Jan 17 '22 at 16:56
  • @rb3652 Be warned that STABLE is more than PERIODIC: "A periodic billiard path on a triangle is called stable if a periodic billiard path of the same combinatorial type exists on all nearby triangles". The combinatorial criterium is needed for stability, but not for periodicity (see the example of $213$ in my answer). – Intelligenti pauca Jan 17 '22 at 17:34
  • Ah, I see. Thank you for the clarification. So really, my algorithm should be implementing the unfolding as the first check, because that's really what determines the periodicity, and only if a path satisfies the unfolding check should it be tested for the combinatorial check (for stability). – rb3652 Jan 17 '22 at 17:36
  • Hi @Intelligenti pauca, I've been thinking a lot about how to go about algorithmically implementing this unfolding process, but with little success. I was wondering if we could discuss this at a mutually convenient time in the "Triangular Billiards Problem" chat room, which I created: https://chat.stackexchange.com/rooms/133555/triangular-billiards-problem-tbp – rb3652 Jan 27 '22 at 15:45