Determine the stability of equilibrium point with Lyapunov function

Question

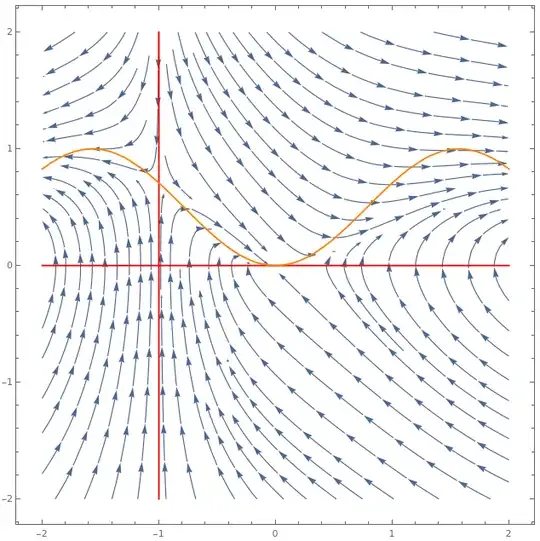
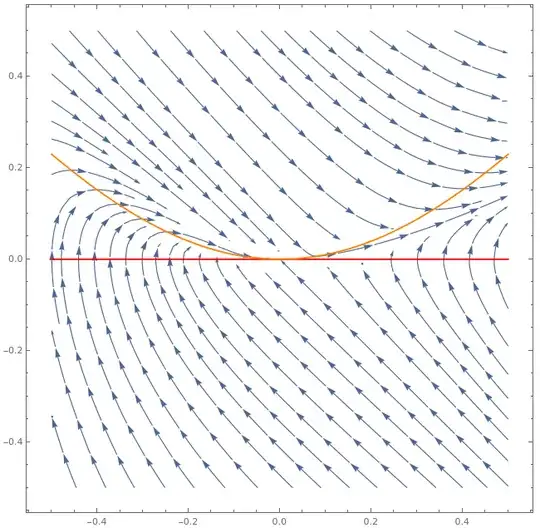
I want to determine the stability of $(0,0)$ (stable, asymptotically stable or unstable) in the nonlinear system:

$$ \begin{aligned} \dot{x} &= y + xy \\ \dot{y} &= -y + \sin^2(x) \end{aligned} $$

---

My attempt

I tried using the eigenvalues of Jacobian evaluated at (0,0), but since

$$\det\left(J_{(0,0)}\right) = \det \begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix} = 0$$

that criterion for evaluating stability does not work, so I then proposed the following Lyapunov function:

$$V(x,y) = \dfrac{1}{2}x^2 + \dfrac{1}{4}y^4$$

then

$$\dot{V}(x,y) = xy + x^2y - y^4 + y^3\sin^2(x)$$

Doing a simple analysis of regions, it is easy to see that

$$\dot{V}(x,y) < 0, \ \mbox{ for } x > 0, \ y < 0$$

I understand that the Lyapunov stability criterion allows us to conclude that $(0,0)$ is stable if $\dot{V}(x,y) \leq 0$ and asymptotically stable if $\dot{V}(x,y) < 0$ for $(x,y) \neq (0,0)$.

My first question is about the previous result, since it is not clear to me whether to conclude the type of stability it is necessary to prove the results for every point $(x,y) \neq (0,0)$ in $\mathbb{R}^2$ or only for any $(x,y) \neq (0,0)$ within a neighborhood $U$.

The second question has to do with my analysis of the behavior of the derivative in a region: in the mentioned region $\{x>0,\ y <0\}$, I could conclude that the derivative is strictly negative, however, for the region $\{x < 0 ,\ y < 0\}$, the derivative can take positive values, can I state, just for the first region, that the (0,0) is asymptotically stable or due to the behavior not necessarily less than or equal to zero of the derivative at $\{x < 0, y < 0\}$, should it be stated that the point is unstable?

The problem is that I have done other Lyapunov stability exercises where it is very simple to verify that, for any point other than the equilibrium point, the derivative $\dot{V} \leq 0$ or $\dot{V} < 0$ and therefore, to conclude the stability of the equilibrium point is simple, however, this exercise has made me realize that maybe I am not understanding well the stability criterion or, I have problem finding a Lyapunov function that is useful for the analysis.

I would appreciate any help you can give me to better understand and conclude my result.

Answer 1

First question: It's enough that $\dot V < 0$ (or $\dot V \le 0$, respectively) in a punctured neighborhood of the origin. Stability is a local notion, after all.

If $\dot V < 0$ for all $(x,y) \neq (0,0)$ and you also have the additional condition that $V(x,y) \to \infty$ as $\sqrt{x^2+y^2} \to \infty$, then you can draw the stronger solution that $(0,0)$ globally asymptotically stable, i.e., it's stable and all trajectories converge to it. (For examples showing why the extra condition is necessary, see this question.)

Second question: From your investigations so far, you can draw no conclusion (neither stability nor instability). The quadrant $\{ x>0, \, y<0 \}$ is not a punctured neighborhood of the origin, so Lyapunov's theorem doesn't apply. You can't even say that the origin is “stable for trajectories starting in that quadrant”. Sure, as long as you're in that quadrant, $V$ will decrease along trajectories, but there's nothing stopping the trajectories from leaving that quadrant and going into regions where you have no control of the sign of $\dot V$.

However, if you simply look at the phase portrait close to the origin (considering the signs of $\dot x$ and $\dot y$), it shouldn't be too hard to realize what the answer is. Here's a plot of the big picture (with the nullclines $\dot x=0$ and $\dot y=0$ in red and orange):

And here's a closeup around the origin (look in particular at the region where $x>0$ and $0 < y < \sin^2 x$):