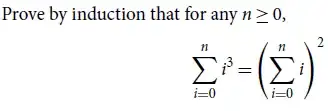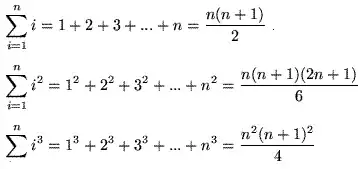what is the approach in this example:
I checked four inputs from zero to 3(included) and got the same output for all of them: 0,1,9,36. I guessed the law that stands behind it, which is:
So i proved the Base Case for n = 1, and assumed Hypothesis that n = k is true.
Solving for the Induction Step i got:
$k(k-1)(k+1)^3$