Following this question How to define $A\uparrow B$ with a universal property as well as $A\oplus B$, $A\times B$, $A^B$ in category theory? I was asking myself if a weaker tetration-like object can be defined category-theoretically.
The point I feel is implicit in the linked answers and comments, and in other similar questions, is that it is highly unlikely that there is a natural higher counterpart of ${}^nb$ that make us recover by "de-categorification" the arithmetic properties of tetration (except for few special case. See: What combinatorial quantity the tetration of two natural numbers represents? or think of the beth function).
In all the cases it seems to me that tetration is taken to be that arithmetic function that is defined recursively by iterating exponentiation, thus in the linked question there is an attempt to iterate internal homs.
I'd try instead to take the fundamental functional equation of tetration and try to replace number by objects, functions by functors and equality by natural transformations.
I have two questions.
$Q1$ Is it possible to find a more reasonable definition of tetration that is more "category-theoretic friendly"? To be more specific, I don't necessarily expect who answers to work out from scratches a reasonable definition so I'll give some definitions myself. This question then can be rephrased as: do my definitions make sense?
When we generalize tetration in the context of iteration theory we get that, let's oversimplify, a tetration function $T:\mathbb R\to\mathbb R$ is a function s.t. $$T(x+1)=b^{T(x)}$$ In the same way, superlogarithms should satisfy, let's ingore domain of definition issues $$S(b^x)=S(x)+1$$
Is think this can be a good starting point to a "categorification" attempt. I know, most of these are probably trivially flawed, but I'll still give a naive try. I hope someone can find holes, or better, fix the definitions.
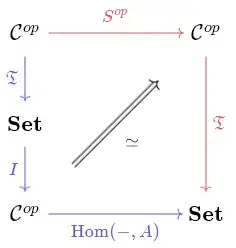
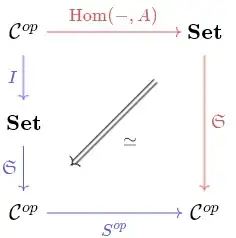
Attempt A. Let $\mathcal C$ be a category and given $I:{\bf Set}\to \mathcal C^{op}$ a functor and $S$ and endofunctor of $\mathcal C$ (think of that as a kind of successor of objects). We say that $\mathfrak T:\mathcal C^{op}\to {\bf Set}$ is a tetration functor iff exists an object $A\in\mathcal C$ and a natural trasformation $$\mathfrak TS(-)\simeq {\rm Hom}(I\mathfrak T(-),A)$$
In the same vein a functor $\mathfrak S$ is a superlogarithm of the object $A$ (relatively to a presheaf $I$) iff exists a natural transformation $$\mathfrak S( {\rm Hom}(-,A))\simeq S\mathfrak SI(-)$$
Attempt B. Let $\mathcal C$ be a closed monoidal category: we say $\mathfrak {tet}$ is a tetration endofunctor iff exists an object $A$ and a natural trasformation $$\mathfrak{ tet}S(-)\simeq [\mathfrak{ tet}(-),A]$$ Here I'm not sure about where to put contraviance and if it is the case to take $S:\mathcal C^{op}\to \mathcal C$ and consider $\mathfrak{ tet}S(-)\simeq [\mathfrak{ tet}^{op}(-),A]$
$Q2$ Maybe all the above attempts are flawed. Anyways it seems to me that the analysis of the properties of tetration, taken to be solution of a functional equation, shows that if we replace numbers by objects, functions by functors, and exponentials by Hom functors (internal or not) give us some interesting expressions. So the last question is: do some of the natural transformations between functors that I tried to write down appear naturally in some context, even in a slightly modified form?