I want to draw a curve on the top of the function $f(x)=1+\dfrac{\sin(x)}{x}$, but the curve should be equidistant (perpendicular distance from any point of the function $f(x)=1+\dfrac{\sin(x)}{x}$) from every point of the curve. Could anyone help in this regard?
Asked
Active
Viewed 164 times
1
-
3It won't necessarily be a function anymore... – J. M. ain't a mathematician May 31 '13 at 10:30
-
Yes, that I realized but it is possible to construct that surface numerically. I don't know how to do this. – sknandi May 31 '13 at 11:30
-
You don't need numerics; you should be able to use the formulae here to derive parametric equations for your parallel curve. – J. M. ain't a mathematician May 31 '13 at 11:32
-
This general problem is called an "offset curve" and can be based on a curve or polygon. This question about bezier offsets may help. – Mark Ping May 31 '13 at 16:37
-
@Mark, though "parallel curve" is the more standard terminology in the mathematical literature... – J. M. ain't a mathematician Jun 01 '13 at 16:39
1 Answers
3
I've arbitrarily decided to be indulgent today, so I'll write out in full how one might generate the parallel curve of a function. Adapting the formulae from the MathWorld link to the case of a function curve, we have the following parametric equations for a parallel curve to $y=f(x)$ with offset $h$:
$$\begin{align*} x&=t\pm\frac{h f^\prime(t)}{\sqrt{1+f^\prime(t)^2}}\\ y&=f(t)\mp\frac{h}{\sqrt{1+f^\prime(t)^2}} \end{align*}$$
For the OP's function, we have, after some simplification,
$$\begin{align*} x&=t\pm\frac{h (t\cos\,t-\sin\,t)}{\sqrt{t^4+(t\cos\,t-\sin\,t)^2}}\\ y&=1+\frac{\sin\,t}{t}\mp\frac{ht^2}{\sqrt{t^4+(t\cos\,t-\sin\,t)^2}} \end{align*}$$
Here's a plot of a bunch of parallels, with the starting curve marked in red:
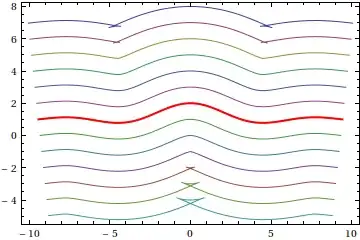
As I've previously noted, for certain values of $h$, the curves are no longer functions, and start displaying cusps. On the other hand, even for the parallels that are still functions, it is rather difficult to obtain an explicit $y=f(x)$ expression, so you may have to be content with the parametric representation.
J. M. ain't a mathematician
- 76,540
-
Thanks a lot J.M. what is the function you have considered in your plot ? – sknandi Jun 12 '13 at 08:53
-
...the function you were asking about. What else could it have been? – J. M. ain't a mathematician Jun 12 '13 at 09:08
-
-
Well, since the discontinuity at $0$ is of the removable kind, I went ahead and defined the value of the function at $0$ to be the same as the value of an appropriate limit. Or, did you not tackle that limit while learning calculus? – J. M. ain't a mathematician Jun 12 '13 at 10:21