How to calculate exponential or logarithmic decay within range over a specified time period?

Question

I am trying to calculate a value over time based on a set of parameters, for example:

start = 0.10
end   = 0
time  = 720

Where time is the desired time for the function to go from the start to the end values.

I have tried to follow some examples and plot them out to see if I am doing it correctly but am not able to get expected results.

For linear decay I cam up with this formula, which behaves as expected:

$rate = (start - end) / time$

$f(t) = start - (rate * t)$

For exponential decay I came up with the formula:

$rate = (start - end) / time$

$f(t) = start - (rate * ln(t))$

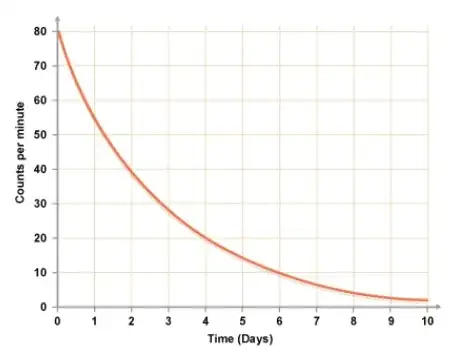
I am clearly not a math genius but in my mind I am trying to get curves that resembles this (in general shape, ignore the axis values):

Exponential Decay:

From the graph I would say that the differential equation is $y^{'}(x)=\frac{a}x$. This is the continuous change, which matches the graph. And the solution is $y(x)=a\cdot \ln(x)+C$, where $a$ and $C$ (integration constant) are parameters which can be specified. — callculus42, Mar 10 '21 at 19:23
@callculus the graph is just a visual aid, not intended to be solved, the basic function I believe is what you have stated although I do not know how to employ that given the parameters I have specified (e.g. what is A and C in my case?) — WerkkreW, Mar 10 '21 at 19:47
Can you give me your conditions in terms of $y(x_0)=y_0$?. For instance, $y(1)=6$ — callculus42, Mar 10 '21 at 19:56
$y(0) = 0.10$ and $y(720) = 0$ in the example parameters I provided — WerkkreW, Mar 10 '21 at 20:18
OK. The problem is, that the domain of $x$ at $y(x)$ is greater than $0$, $x>0$. So it is not possible. — callculus42, Mar 10 '21 at 20:46
To get a solution we can define $y(x)= -\ln(x+b)+C$ with the differential equation $y^{'}=-\frac1{x+b}$. So $y(0)=-\ln(b)+C=0.1$. And $y(720)=-\ln(720+b)+C=0$. The solution is $y(x)=-\ln(x+6846)+8.93142$ — callculus42, Mar 10 '21 at 21:24

0 Answers0