7

I found this proof of Pythagorean Theorem from what 3Blue1Brown shows in his Lockdown math lecture "Trigonometry Fundamentals":

In the following right triangle, project $\cos\alpha$ and $\sin\alpha$ back to the hypotenuse of length $1$, they become $\cos^2\alpha$ and $\sin^2\alpha$: $\to\cos^2\alpha+\sin^2\alpha =1 $.

enter image description here

I thought this is what a simple, visual, and elegant proof! My questions:

  1. Is it a circular proof, why?
  2. If not, are there better ones?

I want clarity about whether or not this proof is circular. The argument only depends on the definition of the sine and cosine functions and nothing more (please correct me if I am wrong). This is why I love it. Many other geometry solutions involve more than three shapes.

Xander Henderson
  • 32,453
Star Bright
  • 2,368
  • 2
    I think there are several hundred proofs of the Pythagorean Theorem. I know a dozen off the top of my head that are far more elegant than this and require no trigonometric functions. A simple Google search will find them. – David G. Stork Mar 08 '21 at 17:18
  • 1
    Elisha Loomis' "The Pythagorean Proposition" (PDF link via ed.gov) has 370 proofs for you to consider. Cut-the-Knot's "Pythagorean Theorem" page has 122. (Of course, there's overlap.) – Blue Mar 08 '21 at 17:21
  • 3
    The definition of $\cos$ and $\sin$ depend ENTIRELY on the Pythagoren Theorem being true so the proof is utterly circular and useless. – fleablood Mar 08 '21 at 17:32
  • 2
    @fleablood By what definition? The usual are something like "$\sin \alpha$ is the ratio of the opposite leg length to the hypotenuse length in a right triangle with one angle $\alpha$". The ratio is easily unique just by similar triangle arguments. The Pythagorean Theorem is not used there. – aschepler Mar 08 '21 at 17:34
  • 1
    But the relationship of $\cos^2 x + \sin^2 x = 1$ depends on, is equivalent to PT. I imagine this image assumes the PT and is used to prove the identity. But you can't assume neither without proof. – fleablood Mar 08 '21 at 17:46
  • " I am not sure it is, since it only depends on the definition of sine and cosine functions and nothing more (please correct me if wrong)" Okay, you are wrong. It depends on the definitions of sine and cosine AND on the relation $\cos^2 x + \sin^2 x = 1$. We can not assume the relation based only on the definitions. – fleablood Mar 08 '21 at 17:48
  • 1
    Okay, I spoke hastily when I said the definitions depend on PT. They don't. I was think thinking the definition depended on the proportionality of similar triangles (which depends on Euclid's 5th posulate-- PT depends equally on those). However the basic trig identity $$\cos^2 x + \sin^2 x = 1$$ is nothing more nor less than a RESTATING of the pythagorean theorem. – fleablood Mar 08 '21 at 17:54
  • 2
    @fleablood That's how it seemed to me at first. No, the proof is not assuming $\sin^2+\cos^2=1$, it's showing that. Look at the picture: The definition of $\sin$ and $\cos$ in terms of triangles shows that those two segments have length $\sin(\alpha)^2$ and $\cos(\alpha)^2$. – David C. Ullrich Mar 08 '21 at 18:50
  • Related, and relevant to @Fleablood 's comments. https://math.stackexchange.com/questions/3566541/is-pythagoras-theorem-a-theorem/3566726#3566726 – Ethan Bolker Mar 09 '21 at 00:23
  • I have made a few edits to your question in order to make it read more like a single, coherent narrative. Meta commentary indicating where edits have been made detract from the question, and any user who really cares about the history of the question can read the edit history. Also, can you please edit your question to provide a link to the video you are asking about? – Xander Henderson Mar 09 '21 at 02:42
  • @Xander Thanks! Done. ( I kind of hesitate to remove the edits for the reason that it may make the discussions in the comment sections seem irrelevant for people not knowing the history. Well, there is always a trade off or balance :-). – Star Bright Mar 09 '21 at 03:03
  • @BrightStar The goal is to incorporate comments into the post so that the comments can be deleted. Comments are meant to be ephemeral, and you should assume that they will all be deleted eventually. And, again, if someone really cares about how the question evolved, they can view the edit history. Explicit indications regarding where edits have been made don't need to be in the question. – Xander Henderson Mar 09 '21 at 03:35
  • 1
    This is the standard proof (converted in language of trigonometry) which is based on the similarity of two smaller triangles sharing the common altitude with the original triangle. This is what I got from my 10th grade textbook. More like old wine in New bottle. And it is not circular. – Paramanand Singh Mar 09 '21 at 03:48

5 Answers5

8

This is a great question. The original proof-as-I-read-it is valid, but some proofs can be "better" or worse in other respects. (By "as I read it", I mean with the implication that it calculates projections with similar triangles as I describe below, rather than stating their values without proof.) There are many criteria for saying one proof is "better" than another, so I'll focus on one germane to this question: making it obvious to all readers that there's no circularity (spoiler alert: there isn't).

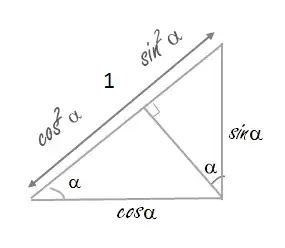
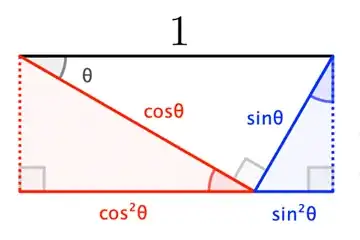
Let the legs adjacent to and opposite $\alpha$ have respective lengths $a,\,b$, and let $c$ denote the hypotenuse's length. By similar triangles, your projections are $c(a/c)^2,\,c(b/c)^2$. Since they sum to the full hypotenuse $c$, $a^2+b^2=c^2$.

Since we define $\cos\alpha,\,\sin\alpha$ respectively as $a/c,\,b/c$, the above calculation can be restated as$$c\cos^2\alpha+c\sin^2\alpha=1\implies c(a/c)^2+c(b/c)^2=1\implies a^2+b^2=c^2,$$which is basically what your proof does. (It takes $c=1$ throughout, but that just changes the units to tidy the algebra; it's not an extra assumption as such, so it covers the general case.) But as I've shown above, there's no need to work with anything other than rational functions of $a,\,b,\,c$. The trigonometric approach switches from such rational functions to something more conceptually advanced, then "uninstalls" the trigonometry later.

One could argue this is a worse proof than the one I've presented, because in taking unnecessary detours it not only asks more of us, it also obscures the underlying reasoning. Well, whether it does is a psychological question, but people mistakenly thinking it's circular suggests as much.

Well, I want to be fair with an edit: as best I can tell from recent comments, those people either didn't realize which proof strategy is implicit in the OP's discussion of projections, or are making the actually salient point that the drawing itself doesn't necessarily communicate that as clearly as one would like in a proof without words. But the facts are these:

  • the proof can easily be spelled out in the aforementioned non-circular way,
  • it takes a bit more work to do that than is obtained in at least some readings of the picture and the text above it, and
  • none of these subtleties matter if we skip the trigonometry altogether, as aforesaid.
J.G.
  • 118,053
7

As nicely compact as the cited diagram is, I might be inclined ---as a matter of diagrammatic pedagogy--- to render things thusly:

enter image description here

This arrangement can help make clear(er) that

  • "$\sin\theta$" and "$\cos\theta$" are effectively definitions (of particular ratios in a right triangle)
  • "$\cos^2\theta$" and "$\sin^2\theta$" are consequences (via proportions in similar right triangles)

so that

  • "$\cos^2\theta+\sin^2\theta=1$" is a deduction, not an assumption.

As a result, some (most? all?) of the confusion about the logical dynamics is mitigated. There's no circular argument here.

(Plus, as a matter of diagrammatic style, I find it's often preferable to avoid overlapping elements.)

The contention (dating back at least as far as to Loomis in the 1940s) that "no trigonometric proof [of the Pythagorean Proposition] is possible" seems to manifest in knee-jerk rejections of any argument that makes any reference whatsoever to sine or cosine. Granted, caution is advised when considering such things: once trig relations become second-nature to us all, it's all-too-easy for an author to inadvertently invoke a Pythagorean identity ... and for a reader to overlook the mistake. But, when caution is applied, it's certainly possible to construct a viable proof.

Blue
  • 83,939
  • 2
    You definitely help to clear the frog, thanks! – Star Bright Mar 09 '21 at 02:40
  • Ribbit! ....... – Blue Mar 09 '21 at 02:45
  • This is great! I was reading "On the Possibility of Trigonometric Proofs of the Pythagorean Theorem" linked in your question on HSM, but this proof is much more beautiful (although perhaps less general) than the one presented there – Vincent Nov 05 '24 at 17:13
  • @Vincent: Thanks! :) ... BTW: I posted to HSM to obtain primary source material about Versluys' proof in order to complete this answer to (yet) another question about trigonometric proofs of Pythagoras. – Blue Nov 06 '24 at 10:04
3

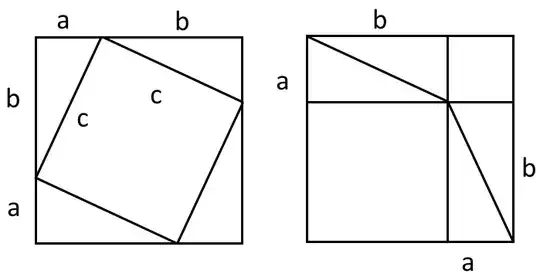Filling an <span class=$(a+b) \times (a+b) $ square" />

You can see above two squares of side $(a+b)$ filled with some squares and triangles. Can you spot the visual proof of Pythagorean Theorem behind these pictures?

Andrea Marino
  • 6,166
2

Elegance is in the eye of the beholder.

Your proof is simple. But I think to be elegant it should also be tangible and convincing. If we divide a hypotenuse of $1$ into two segments $x$ and $y$, it's simple clear and convincing that by similar triangles that the proportions $x:: \cos \alpha$ and $\cos\alpha:: 1$ are equal and $y :: \sin \alpha $ and $\sin\alpha :: 1$ are equal.

ANd from there the algebra that $x = \cos^2 \alpha$ and $y = \sin^2 \alpha$ is clear and simple so the result $1 = x + y = \cos^2 \alpha + \sin^2 \alpha$ is immediate.

But, at least to me, just what the algebra is saying isn't tangible or obvious and is quite abstract. I can convince myself of it. It means that the area $\cos \alpha \times \cos \alpha$ square has the same the area of a $x \times 1$ rectangle but... well, it's easy to loose it. I find myself second guessing "wait, what does area mean again when we aren't talking of integers? And I don't want to rely on limits and real analysis where are we again?" Somehow we have turn linear measurements to area measurements being convertible and ...

I find proofs like Andrea Marino's far more tangible (and, yes, I can go through the same existential questions of what is area; but in that type of proof I'm not compelled to). However.... maybe it's too practical and not abstract enough to be elegant.

The more I think and worry of the abstraction, the more I'm compelled to prefer a Euclid like proof of comparing two sets of rectangles, parallegrams, and squares. .... But I can hardly call those simple or elegant.

fleablood
  • 130,341
0

Harry Helson showed us this proof my first semester at Berkeley, using the dot product: $(x+y)\cdot(x+y)=x\cdot x+y\cdot y+2x\cdot y$, which gives the result when $x$ and $y$ are perpendicular.

I like even better the one where a square of side length $c$, the hypotenuse, is offset in a square of side length $a+b$, the sum of the lengths of the legs.