My question is an extension to a previous question I posed on stack : Measure change in angle during rotation of quaternion . While there is a split between robotics and programming, my question is primarily around math. In my previous effort, I wanted to observe angular displacement as my robot was picking up boxes. I solved my problem by establishing a static reference, $q_s$, and measured change in angle from each incoming quaternion my robot was sharing, $q_n$.
\begin{equation} q = [s, \boldsymbol{v}] \quad s \in \mathbb{R}, \boldsymbol{v} \in \mathbb{R}^3 \end{equation}
Since the rotation occurs on the z-axis, I normalize and zero out the $y$ and $x$ components of $v$. The product of $q_s$ and $q_n^*$ allows me to compute the angle, being $2 * acosd(s)$.
\begin{equation} q_n^* = [s, - \boldsymbol{v}] \end{equation}
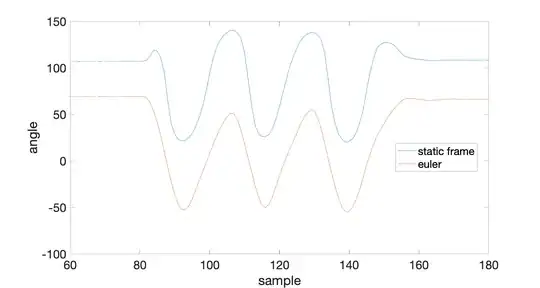
When I apply this procedure to my robot and compare it against the Euler rotation, I get very similar results. They are demonstrated in the image below, where the blue line represents results using a static frame ($q_s$) and the red line Euler rotation (pitch). The results mostly look good to me, excluding the bumps at samples $\approx 80$ and $\approx 150$. These can easily be solved by changing the direction of rotation.
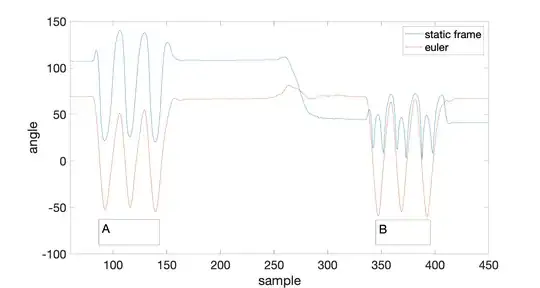
Using a static frame of reference ($q_s$) does not work well when my robot moves around the warehouse. For example, imagine a robot is standing in front of you and picks up a box and puts it back on the ground. By doing so, the robot will generate the pattern above. Let's refer to this position as $A$. Now, the robot rotates $\approx 90^{\circ}$ on the x-axis to your right and performs the same task using a box facing your friend. Let's refer to this as position $B$. If I run the same computation as above, I see the following pattern. (Note: the transition from A to B occurs at sample $\approx 250$)
The angular displacement using $q_s$ looks odd at first as it drifts ``down''. Notice the decline in the angle at sample $250$ that is present when using quaternions but not Euler rotations. However, this does make sense. When I look at the unit circle and compare the distance between $q_s$ and $q_n$, the change in position causes a change in angular displacement. This evidence suggests to me that a static reference frame ($q_s$) is only good if my robot does not change position (never turns to your friend, only looks at you). If I were to adjust for the change in position, I could devise a more appropriate $q_s$ from which I can measure change.
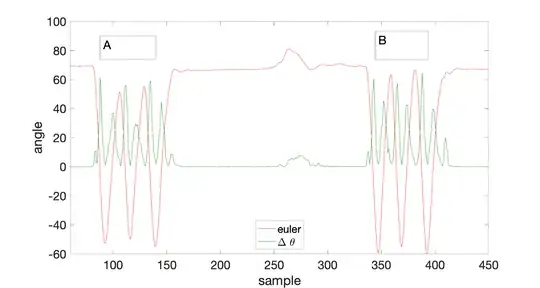
Instead of using $q_s$, I then explored comparing angular displacement between $q_n$ and $q_{n-1}$. My product is then computed using $q_{n-1}$ and $q_n^*$, where $\Delta \theta$ is the relative difference in angle between neighboring quaternions. In my mind, I get a picture that the frame of reference would continuously update. If I run this, I can generate the following graph, where the green line uses adjacent quaternions and red line Euler rotations:
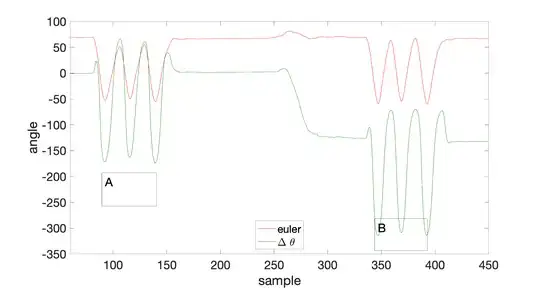
The drift is no longer present at $250$ and the rotation is always positive. Both of these results so far make sense. However, I cannot seem to figure out how to use $\Delta \theta$ to construct the sinusoidal-like pattern. Since this is possible using Euler rotations I do not see why I cannot accomplish it using quaternions. Unfortunately, I find myself writing ``rules'' on how to interpret every incoming $\Delta \theta$. For example, let's assume that I store every $\Delta \theta$ in a vector $r$. I would then calculate current $r$ by adding $r-1$ to current $\Delta \theta$. $\Delta \theta$ can be negative or positive depending on which quadrant it falls within. If I do so, I can generate a graph like this:
However, I then recreate the same problem I experience when using $q_s$. It is clear from Euler rotations and even using a static reference frame that my robot can generate the same pattern when lifting a box. It is only the change in the robot's position that causes issues. What is the correct way to measure the change in angular displacement when the frame of the reference can be influenced by position (A -> B)?
Note: In reading this book, the author mentions that a frame can be rotated around a vector, p: $q^-1 pq$. This might be the right way to adjust $q_s$. However, no further comments are made on how I can construct p.