Solve Least Squares with Tikhonov Regularization Linear Equality and Non Negative Constrains

Question

How to solve the following constrained minimization problem: $$ \arg_S min_\; \frac{1}{2}\left \{ \left \| K_2SK_1^T-M \right \|_F^2 +\lambda \left \| S \right \|_F^2\right \} \\ s.t. \sum_{1}^{col}S=Sum1 \\ \sum_{1}^{row}S=Sum2 \\ s_{i,j} \in S \geq 0 \\ $$

where $K_1$,$K_2$,$M$ and $S$ are 2d Matrix, and only $S$ is unknown. In the constraints, $Sum1$ is the sum along the column of $S$, which is a row vector. $Sum2$ is the sum along the row of $S$, which is a column vector. All elements in $S$ are non-negative.

Here is the data stored in mat format. How to solve this kind of problem? Are there any MATLAB routines I can use out-of-box?

    load('matlab.mat');
%　 min norm( K2*X*K1'-M,'fro')^2+lambda*norm(X,'fro')^2
%   s.t. sum(X,1) = Sum1 ;   sum(X,2) = Sum2; all(X>=0) = true

What I've Tried:

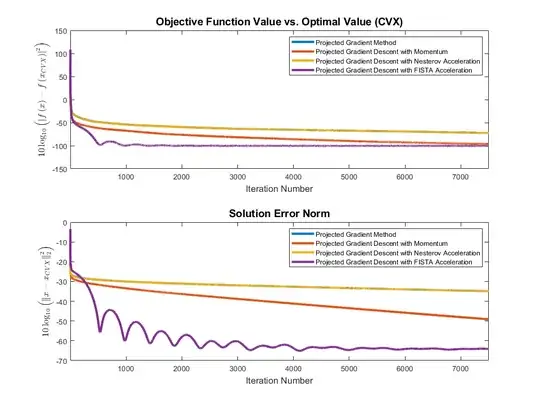
• CVX:

Failed to find the optimal solution with all supported solvers. Here is the cvx script I use:

cvx_begin
variable S(size(K2,2),size(K1,2))
minimize(0.5*(square_pos(norm(K2*S*K1'-M,'fro'))+lambda*square_pos(norm(S,'fro'))))
sum(S,1) == Sum1
sum(S,2) == Sum2
S>=0
cvx_end

Edit:

A synthetic data with much smaller scale was attached here. DR was also normalized.

Answer 1

The Objective Function is given by:

$$\begin{aligned} \arg \min_{S} \quad & \frac{1}{2} {\left\| {K}_{2} S {K}_{1}^{T} - M \right\|}_{F}^{2} + \frac{\lambda}{2} {\left\| S \right\|}_{F}^{2} \\ \text{subject to} \quad & {S}^{T} \boldsymbol{1} = \boldsymbol{u} \\ & S \boldsymbol{1} = \boldsymbol{v} \\ & S \geq 0 \end{aligned}$$

While one could use many specialized solvers for the above problem I'd start with the Projected Gradient Descent.
In order to use the Projected Gradient Descent we need the projection onto the intersection of all 3 constraints sets. Yet, since the set $ \left\{ S \mid S \geq 0 \right\} $ isn't a sub space we can't use the alternating projection method (See Projections onto Convex Sets and Projection of $ z $ onto the Affine Half Space $ \left\{ x \mid A x = b, \; x \geq 0 \right\} $). It can be solved using the Dykstra's Projection Algorithm from Orthogonal Projection onto the Intersection of Convex Sets.
The Dykstra's Projection Algorithm requires the projection onto each set to generate an iterative algorithm to computer the projection onto the intersection of all sets.

Hence, the atoms of the projected gradient Descent are:

1. The Gradient of the objective function: $ {K}_{2}^{T} \left( {K}_{2} S {K}_{1}^{T} - M \right) {K}_{1} + \lambda S $.
2. Projection onto the 1st constraint: $ \operatorname{Proj}_{ \left\{ X \mid {X}^{T} \boldsymbol{1} = \boldsymbol{u} \right\} } \left( Y \right) = Y - \boldsymbol{1} \frac{ \boldsymbol{1}^{T} Y - \boldsymbol{u}^{T} }{ \boldsymbol{1}^{T} \boldsymbol{1} } $.
3. Projection onto the 2nd constraint: $ \operatorname{Proj}_{ \left\{ X \mid X \boldsymbol{1} = \boldsymbol{v} \right\} } \left( Y \right) = Y - \frac{ Y \boldsymbol{1} - \boldsymbol{v} }{ \boldsymbol{1}^{T} \boldsymbol{1} } \boldsymbol{1}^{T} $.
4. Projection onto the 3rd constraint: $ \operatorname{Proj}_{ \left\{ X \mid X \geq 0 \right\} } \left( Y \right) = \max \left( Y, 0 \right) $.

Remark: Since $ \boldsymbol{1} $ is a vector of ones (With the appropriate dimension in each use above) the projections steps could be optimized. For example $ \boldsymbol{1}^{T} \boldsymbol{1} = m $ or $ \boldsymbol{1}^{T} \boldsymbol{1} = n $ (Number of rows / columns) and using sum() and repamt() to imitate the multiplication by the vector.

I implemented the solution in MATLAB and got the following results compared to CVX:

The iterative methods are slower than CVX for this task (I used MOSEK).
Yet, this is on small size of the data. Probably they will be able to be faster for large scale problem (Still you'll have to give a solver a lot of time to get the result).

I'd also recommend adding Line Search. As this problem is not well poised.