How can I fold paper into 3 x 4 grid? Or prove that it can't be done?

Question

I am trying to fold paper so that it looks like 3 x 4 grid of 12 rectangles of equal size.

Like this https://www.wolframalpha.com/input/?i=3+x+4

Its easy to get 4 rectangles. Just fold twice. But how to get 3?

The Pythagoras theorem may help $3^2+4^2=5^2$ is the relationship b/w sides of a right triangle. — DVD, May 16 '13 at 06:55
http://math.stackexchange.com/questions/736346/how-can-a-piece-of-a4-paper-be-folded-in-exactly-three-equal-parts
This would help you divide it into 3 parts — Harshal Gajjar, Apr 05 '14 at 07:43
This question was asked before that question so that one is duplicate of this one :D lol — Pratik Deoghare, Apr 05 '14 at 18:18

score 4 · Answer 1 · answered May 16 '13 at 06:09

4

Let the paper be $[0,a]\times[0,b]$ By halving you find $(\frac a2,0)$, make a crease to find the line through $(\frac a2,0)$ and $(0,b)$. This intersects the diagonal at $(\frac a3,\frac b3)$.

answered May 16 '13 at 06:09

Hagen von Eitzen

382,479

score 2 · Answer 2 · answered May 16 '13 at 06:15

2

http://upload.wikimedia.org/wikipedia/commons/8/8d/Haga_theorem_1.svg

If your piece of paper is a square ABCD of side length 1, then from the diagram, if AP=1/2, then QC=1/3.

answered May 16 '13 at 06:15

score 2 · Answer 3 · edited Apr 13 '17 at 12:20

2

(Stealing from Hagen von Eitzen's answer and Ross Millikan diagram at How can a piece of A4 paper be folded in exactly three equal parts?)

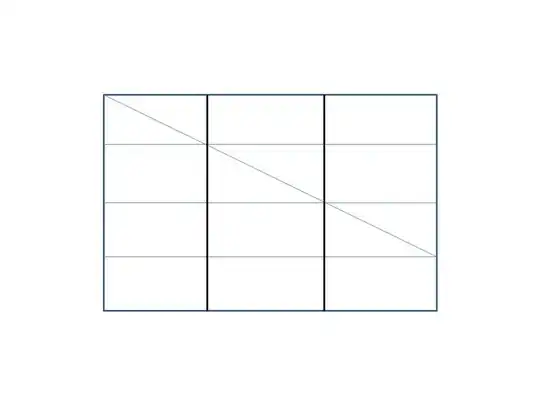
Graphical representation of the folds

Fold the paper into four equal horizontal strips with two folds
Fold a diagonal across the top three horizontal strips
Fold vertical strips at the two points where the diagonal crosses the horizontal strips.

edited Apr 13 '17 at 12:20

Community

1

answered Apr 03 '14 at 09:22

Henry

169,616

How can I fold paper into 3 x 4 grid? Or prove that it can't be done?

3 Answers3