Let's say that I have the following data:
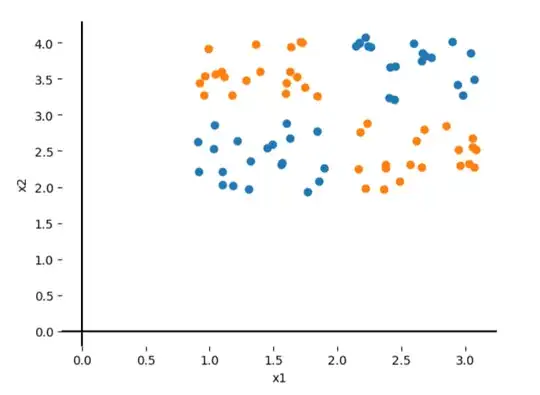
I want to find a transformation of this dataset that will make it linearly separable. My thought was to bring the data around the origin and then multiply $X_1$ by $X_2$ to get the blue data on one side and the orange data on one side. the transformation would be given by $$\phi(X_1,X_2) \rightarrow (X_1,X_2,(X_1-\mu1)(X_2-\mu2)).$$
However, I can't get to find the kernel of this transformation. If I try to do the dot product between $\phi(X_1,X_2) \phi(Y_1,Y_2) $ I don't get a kernel.
What could be a good kernel to achieve such
transformation?
EDIT: I think a good kernel could be the RBF kernel but I am not sure how to apply it. Any thoughts?