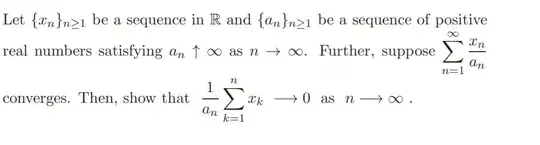My work: Since $\sum\limits_{n=1}^{\infty}\frac{x_n}{a_n}$ is convergent, so its sequential partial sum, denoted by $S_n=\sum\limits_{k=1}^{n}\frac{x_k}{a_k}$ is convergent. Now using Cauchy criteria for series convergence, there exists $n>m\geq N$ such that for any given $\epsilon>0$, we have $|S_n-S_m|<\epsilon$ for all $n>m\geq N$. Now for $n>N$, $$|\frac{1}{a_n}\sum\limits_{k=1}^{n}x_k|=|\frac{1}{a_n}(\sum\limits_{k=1}^{N}x_k+\sum\limits_{k=N+1}^{n}x _k)|=|\frac{1}{a_n}(\sum\limits_{k=1}^{N}x_k+\sum\limits_{k=N+1}^{n}a _k(S_k-S_{k-1}))|$$
I know that $\frac{1}{a_n}(\sum\limits_{k=1}^{N}x_k)$ goes to zero as $n\rightarrow\infty$. How can I estimate the second summation. We also given that $a_n$ is monotonocally increasing positive sequence.
Please give some hint or idea.