2

The divergence a 2D vector Field $\mathbf{F}(x,y) = F_x(x,y)\, \hat{i} + F_y(x,y)\, \hat{j}$ is defined as $$\mathrm{div}\,\mathbf{F} = \bigg( \dfrac{\partial F_x}{\partial x} + \dfrac{\partial F_y}{\partial y}\bigg).$$ This can be calculated IF a function $\mathbf{F}(x,y)$ is given.

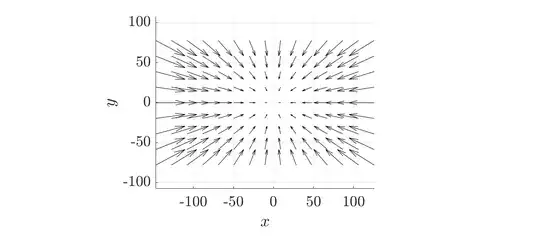
How do I compute the divergence if I don't know the function $\mathbf{F}(x,y)$ that describes my vector field but rather I have an array of numbers (noisy) that form a vector field as depicted below.

enter image description here

I know only the $(x,y)$ coordinates of the tip and the tail of each vector. Just by looking at the picture below, the field has a negative divergence. How can one calculate the divergence of such a field?

Note: This is a part of the problem addressed here

unfinished_sentenc
  • 77
  • Thanks for pointing out the typo. – unfinished_sentenc Sep 30 '20 at 17:05
  • Since you know your data is "noisy", it makes sense to try smoothing it before trying to do numerical differentiation. A typical approach (see here) is to fit a polynomial to local data points, much like a moving average. It is fortunate that you do not need more than first (partial) derivatives to estimate divergence. – hardmath Sep 30 '20 at 17:56
  • Is smoothing done to make the field differentiable? How do I algebraically express the divergence equation in this case for 2 point clouds each with $M\times N$ entries of the coordinates? – unfinished_sentenc Sep 30 '20 at 18:48
  • As you can guess from the picture, the points are moving further away along $z-$axis. If it were to move towards the observer, the vectors would point outwards. My goal is to first find the divergence and using it find the translation amount along $z-$axis. Then translate the points (by the amount from divergence) such that the field vanishes. – unfinished_sentenc Sep 30 '20 at 18:56
  • You described the array of numbers as noisy, and numerical differentiation will amplify that noise. Thus smoothing is suggested as a means of mitigating the noisiness of your data. Experimentation is needed to see if results that suit your application are possible. – hardmath Sep 30 '20 at 19:33

1 Answers1

1

You can use the divergence theorem to approximate the divergence and prevent noise from ruining your approximation.

We have $$\int_C \mathbf{F} \cdot d\mathbf{S} = \int_A (\text{div} \mathbf{F}) dA$$ where the left hand side integral is over the boundary $C$ of any sufficiently nice set $A$ and the right hand side integral is over the set $A$.

Now consider a small area $A$ surrounding the point $p$ and assume that you know $\mathbf{F}$ at some points $q_i$ of $C$. You can then approximate the left integral using the a weighted sum of the $\mathbf{F}(q_i)$. The integral on the right is approximately $ A \text{div} \mathbf{F}(p)$.

Your graph suggests that you know $\mathbf{F}$ on a uniform grid with square cells. For each cell with corners $a_i$ you can find a new cell such that $a_i$ marks the middle of the $i$th edge of the new cell and the outward normal is well defined at $a_i$. You need to rotate 45 degrees to get the new cell. Use the new cell to compute an approximation for the divergence at the center of the new cell.

Carl Christian
  • 13,666
  • To make things more general and simplify things I created $\mathbf{F}$ on a uniform grid. In reality my measured data $(\mathbf{F})$ is non-uniformaly spaced. I am somewhat overwhelmed by the literatures on dealing with vector field on non-uniform grid. How do I compute the divergence if the grid is non-uniform? Any recommendations of books or papers on this subject? Thanks!!! : ) – unfinished_sentenc Oct 22 '20 at 08:51
  • @unfinished_sentenc This is outside my area of expertise, I cannot give you good references. – Carl Christian Oct 23 '20 at 09:38