Finite State Automata

Question

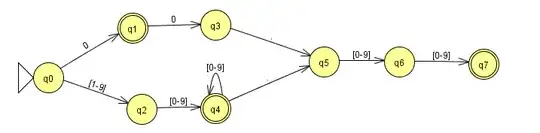
it's been a while since I've done FSA's so I'm a little rusty, bear with me.

I'm creating an FSA to parse Integer and Decimal tokens for a class. The two tokens have the regex

Integer: $0|[1-9][0-9]^*$\
Decimal: $(0|[1-9][0-9]^*).[0-9][0-9]$

Question Prompt: Draw one finite state automaton (FSA) which will scan INTEGER and DECIMAL tokens and discard all other characters read. Note that the scanner will be called repeatedly from the parser and therefore when a string such as 00 is scanned, the second 0 symbol should not be discarded by the scanner.

There are a handful of constraints I have to meet which are:

1. One FSA for both tokens
2. Each type of token must be accepted by it's own single final state
3. The automaton will halt on final states so there are no transitions starting from any final state
4. For each final state, you must indicate next to the state which type of token it accepts and whether or not the last character read to enter the state should be consumed
5. Every state in your FSA should have an "other" transition to capture what happens when any other character than the ones for which you already have a transition is read.

So far I have been reviewing how FSA's work and have drawn up a pretty rough one that I know isn't correct.

Note: The two connections leading to state $q5$ are ".", it might be hard to see in the screenshot

I did my best to combine the two expressions and come up with the above FSA. I'm aware that it probably isn't correct but I can't seem to figure out where to go from here. I appreciate any help I can get, I'd prefer if I wasn't just given the answer as I'd like to learn how to get to it myself :).