If we enumerate uniform polytopes generated by Coxeter diagrams, we find many cases where two apparently distinct Coxeter diagrams yield the same uniform polytope.
A small handful of examples:
- the rectified tetrahedron
 is the same as the octahedron
is the same as the octahedron 
- the cantellated 16-cell
 is the same as the rectified 24-cell
is the same as the rectified 24-cell 
- the cube
 is the same as a square prism
is the same as a square prism  or the product of three segments
or the product of three segments 
- the hypercube
 is the same as:
is the same as:
In none of the above cases is the equivalence obvious to me, from looking at the symbols. How can one recognize it?
One can, of course, use "brute force": that is, construct the two polytopes, and compare their structures.
But is there a simpler / more principled way to recognize equivalence, by just analyzing the graph structure of the two diagrams?
Here's a start.
Answer for 3-node Coxeter diagrams:
The uniform polyhedron or planar tiling generated by a 3-node Coxeter diagram can be unambiguously specified by its vertex configuration; that is, the cyclic list of regular polygons surrounding any vertex.
Therefore, to decide whether two 3-node Coxeter diagrams generate the same polyhedron or tiling, it suffices to compare the two vertex configurations.
Translation from 3-node Coxeter diagram to vertex configuration is summarized by the following table, where $p,q,r \geq 2$, and any $2$'s appearing in the vertex configuration should be removed.
$$ \require{HTML}\newcommand{\mypic}[4][]{\style{display: inline-block;background: url(https://i.sstatic.net/#4) no-repeat center;#1}{\phantom{\Rule{#2}{#3}{0px}}}} \begin{array}{ccc}\hline\text{Case}&\text{Coxeter diagram}&\text{Vertex configuration}\\\hline \text{1 ringed node}&\mypic{36px}{34px}{hVoci.png}&(p\cdot q)^r\\ \text{2 ringed nodes}&\mypic{36px}{34px}{nDAmp.png}&p\cdot2r\cdot q\cdot2r\\ \text{3 ringed nodes}&\mypic{36px}{34px}{k26a3.png}&2p\cdot2q\cdot2r\\\hline\end{array}\\ \text{} $$
Coxeter diagrams with 4 or more nodes?
It seems that the method described above for 3 node diagrams could, in theory, be used for higher dimensions; but unfortunately the vertex configuration isn't as easy to describe and work with, since it's not just a cyclic list of regular polygons, so it's not clear how to proceed.
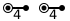

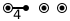

(•)-4-•---•has char. simplex that is 1/48 of the sphere, whereas when expressed as(•) (•) (•)it has char. simplex that is 1/8 of the sphere. – Don Hatch Sep 28 '20 at 09:44